| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- httr
- 하둡
- 하계인턴
- KT AIVLE
- 머신러닝
- 기계학습
- kaggle
- arima
- 지도학습
- 프로그래머스
- 가나다영
- 에이블스쿨
- cnn
- 한국전자통신연구원 인턴
- 딥러닝
- SQLD
- 소셜네트워크분석
- ML
- Eda
- kt aivle school
- KT 에이블스쿨
- matplot
- dx
- SQL
- Ai
- ETRI
- 서평
- 빅데이터분석기사
- r
- 웹크롤링
- 다변량분석
- 시계열
- ggplot2
- hadoop
- 빅분기
- 시각화
- 한국전자통신연구원
- 에트리 인턴
- python
- 에이블러
- Today
- Total
소품집
[DL] 퍼셉트론, 인공 신경망 기본 본문
Perceptron
인공 신경망은 수많은 머신 러닝 방법 중 하나이다. 딥 러닝을 이해하기 위해서는 우선 인공 신경망에 대한 이해가 필요한데, 이번 챕터에서는 초기의 인공 신경망인 퍼셉트론(Perceptron)에 대해서 이해할 필요가 있다.
1. 퍼셉트론 (Perceptron)
퍼셉트론(Perceptron)은 인공 신경망으로 다수의 입력으로부터 하나의 결과를 내보내는 알고리즘입니다. 퍼셉트론은 실제 뇌를 구성하는 신경 세포 뉴런의 동작과 유사합니다. 뉴런은 가지돌기에서 신호를 받아들이고, 이 신호가 일정치 이상의 크기를 가지면 축삭돌기를 통해서 신호를 전달합니다.

이제 다수의 입력을 받는 퍼셉트론의 그림을 보겠습니다. 신경 세포 뉴런의 입력 신호와 출력 신호가 퍼셉트론에서 각각 입력값과 출력값에 해당됩니다.


위 그림에서,
- $x1$ 과 는 입력 신호, $y$는 출력 신호, $w1$과 $w2$는 가중치(weight)를 의미한다.
- 원을 노드라고 부른다.
- 입력 신호가 뉴런에 보내질 때는 각각 고유한 가중치($w1x1, w2x2)$가 곱해진다.
- 뉴런에서 전달 받은 신호의 총합이 임계값 $θ$를 넘을 때만 $1$을 출력한다.
- 각각의 입력값에는 각각의 가중치가 존재하는데, 이때 가중치의 값이 크면 클수록 해당 입력 값이 중요하다는 것을 의미한다.
각 입력값이 가중치와 곱해져서 인공 뉴런에 보내지고, 각 입력값과 그에 해당되는 가중치의 곱의 전체 합이 임계치(thersehold)를 넘을면 종착지에 있는 인공 뉴런은 출력 신호로서 1 을 출력하고, 그렇지 않을 경우에는 0을 출력한다. 이러한 함수를 계단 함수(Step function)라고 하며, 아래 그래프는 계단 함수의 하나의 예를 보여준다.

이때 계단 함수에 사용된 이 임계치 값을 수식으로 표현할 때는 보통 세타($θ$)로 표현합니다. 이를 식으로 표현하면 다음과 같다.
$if \sum_i^{n} W_{i}x_{i}\ < \theta → y=0$$if \sum_i^{n} W_{i}x_{i}\ ≥ \theta → y=1$
단, 위의 식에서 임계치를 좌변으로 넘기고 편향 $b$(bias)로 표현한다. 편향 $b$ 또한 퍼셉트론의 입력으로 사용된다. 보통 그림으로 표현할 때는 입력값이 1로 고정되고 편향 $b$가 곱해지는 변수로 표현된다.
$if \sum_i^{n} W_{i}x_{i} + b < 0 → y=0$
$if \sum_i^{n} W_{i}x_{i} + b < 0 → y=0$

2. 단순한 논리회로
AND Gate
AND 게이트는 입력이 2개, 출력이 1개인 대표적인 퍼셉트론으로 나타낼 수 있는 예시이다. 위와 같은 대응표를 진리표라고 하는데 입력이 모두 1일 때만 1을 출력하고, 그 외에는 0을 출력한다. 이 AND 게이트를 퍼셉트론으로 표현하고 싶을 때 가중치 (w1, w2)와 임계값을 정하는 일이다.

예를들어 (w1, w2, θ)이 (0.5, 0.5, 0.8) or (1, 1, -1)인 경우를 생각해보자.
식 1에 의해 계산해보면
(00.5) + (00.5) = 0.0 < 0.8 -> 0
(00.5) + (10.5) = 0.5 < 0.8 -> 0
(00.5) + (00.5) = 0.5 < 0.8 -> 0
(10.5) + (10.5) = 1.0 > 0.8 -> 1
이렇게 AND 게이트의 값을 만족한다.
이러한 (w1, w2, θ) 경우의 수는 무수히 많다.
NAND Gate and OR Gate


NAND 게이트는 즉 AND에 NOT 연산을 한 것이다. NAND 게이트도 마찬가지로 진리표의 값을 만족하는 (w1, w2, θ) 순서쌍이 존재한다. 예를들어 (-0.5, -0.5, -0.7) or (-0.5, -0.5, 1)등이 있다.
OR 게이트는 입력 신호 중 하나 이상이 1이면 출력이 1이 되는 논리회로이다. 이 게이트를 만족하는 (1, 1, -0.5) or (3, 3, 2) 등이 있다.
이와 같이 퍼셉트론으로 AND, NADN, OR 논리회로를 표현 할 수 있다. 가장 중요한 점은 퍼셉트론의 구조는 모든 게이트에서 같다는 점이고, 다른 것은 매개변수(가중치, 임계값) 뿐이다.
3. 퍼셉트론의 한계
지금까지 단층 퍼셉트론은 AND, NAND, OR 게이트를 구현할 수 있었지만, 단층 퍼셉트론으로 구현이 불가능한 XOR 게이트가 있다. XOR 게이트는 입력 값 두 개가가 서로 다른 값을 갖고 있을때에만 출력값이 1이 되고, 입력값 두 개가 서로 같은 값을 가지면 출력값이 0이 되는 게이트이다.
아무리 많은 가중치와 편향을 넣어봐도 XOR 게이트를 구현하는 것은 불가능하다. 그 이유는 단층 퍼셉트론은 직선 하나로 두 영역을 나눌 수 있는 문제에 대해서만 구현이 가능하기 때문이다.
예를 들어 AND 게이트에 대한 단층 퍼셉트론을 시각화해보면 다음과 같다.
그림에서는 출력값 0을 하얀색 원, 1을 검은색 원으로 표현
AND 게이트를 충족하려면 하얀색 원과 검은색 원을 직선으로 나누게 되고, 마찬가지로 NAND 게이트나 OR 게이트에 대해서도 시각화를 했을 때 직선으로 나누는 것이 가능하게 된다.

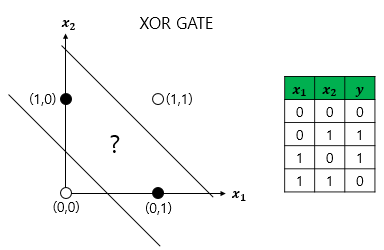
XOR 게이트를 시각화해보면 다음과 같다.
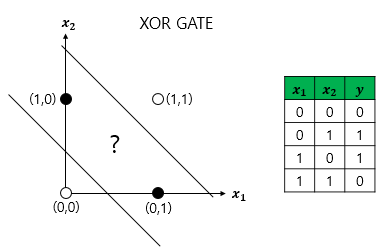
하얀색 원과 검은색 원을 하나의 직선으로 나누는 것은 불가능하다. 즉, 단층 퍼셉트론으로는 XOR 게이트를 구현하는 것이 불가능하게 된다. 이를 단층 퍼셉트론은 선형 영역에 대해서만 분리가 가능하다고 말할 수 있게 되고, 다시 말하면 XOR 게이트는 직선이 아닌 곡선. 비선형 영역으로 분리하면 구현이 가능하다.

4. 다층 퍼셉트론 (MultiLayer Perceptron, MLP)
XOR 게이트는 기존의 AND, NAND, OR 총 3개의 게이트를 조합하면 만들 수 있다. 다층 퍼셉트론과 단층 퍼셉트론의 차이는 단층 퍼셉트론은 입력층과 출력층이 존재하지만, 다층 퍼셉트론은 중간에 층을 더 추가하였다는 점이다.이렇게 입력층과 출력층이 존재하지만 사이에 존재하는 층을 은닉층(Hidden Layer)라고 한다.


위와 같이 은닉층이 2개 이상인 신경망을 심층 신경망(Deep Neural Networ, DNN)이라고 한다. 심층 신경망은 다층 퍼셉트론만 이야기 하는 것이 아니라, 여러 변형된 다양한 신경망도 은닉층이 2개 이상이 되면 심층 신경망이라고 한다.
참조
https://wikidocs.net/24958
https://eehoeskrap.tistory.com/137
'AI' 카테고리의 다른 글
| [DL] CNN Convolution(padding, stride) (0) | 2021.09.30 |
|---|---|
| [DL] 배치(batch)와 에포크(epoch), 반복(iteration) (0) | 2021.09.30 |
| [Kaggle] 영업사원 통장 입금 내역 시각화 (0) | 2021.02.03 |
| [python] pandas 패키지 모음 (0) | 2020.10.16 |
| [Dacon] 심리 성향 예측 AutoML 따라하기 (0) | 2020.10.15 |

