| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
- ML
- 한국전자통신연구원
- 서평
- SQL
- ggplot2
- 가나다영
- 한국전자통신연구원 인턴
- SQLD
- 에이블스쿨
- kt aivle school
- Ai
- 시각화
- arima
- ETRI
- Eda
- 다변량분석
- 에이블러
- cnn
- 빅분기
- 기계학습
- hadoop
- 빅데이터분석기사
- python
- 소셜네트워크분석
- 프로그래머스
- matplot
- 시계열
- KT 에이블스쿨
- 에트리 인턴
- KT AIVLE
- r
- 웹크롤링
- dx
- 하둡
- 딥러닝
- kaggle
- 하계인턴
- 지도학습
- httr
- 머신러닝
- Today
- Total
소품집
[python] SHAP (SHapley Additive exPlanations), 설명 가능한 인공지능 (2) 본문
1. Shapley Value
- Shapley Value란, 게임이론을 바탕으로 Game에서 각 Player의 기여분을 계산하는 방법임.
- 하나의 feature에 대한 중요도를 얻기 위해 다양한 feature의 조합을 구성하고, 해당 feature의 유무에 따른 평균적인 변화를 통해 얻은 값임.
- 따라서 Shapley Value는 전체 성과(판단)을 창출하는 데 각 feature가 얼마나 공헌했는지 수치로 표현할 수 있음.
✔️ 게임이론
여러 주제가 서로 영향을 미치는 상황에서 서로가 어떤 의사결정이나 행동을 하는지에 대해 이론화한 것

- ϕi : i 데이터에 대한 Shapley Value
- F : 전체 집합
- S : 전체 집합에서, i 번째 데이터가 빠진 나머지의, 모든 부분 집합
- fS∪i(xS∪i) : i 번째 데이터를 포함한 (=전체) 기여도
- fS(xS) : i 번째 데이터가 빠진, 나머지 부분 집합의 기여도
Example
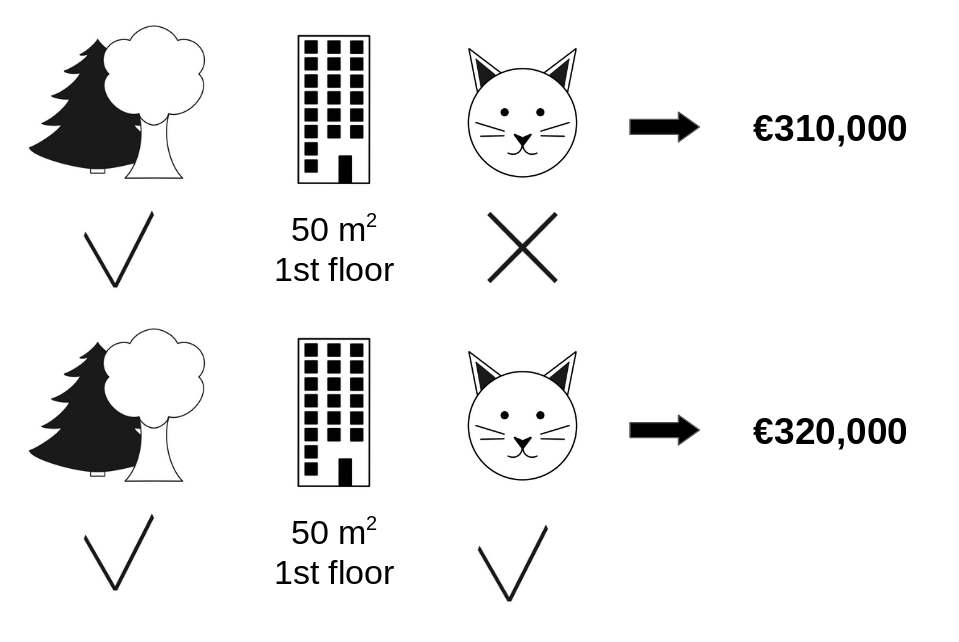
- 집 값을 결정짓는 요인으로 [숲세권, 면적, 층, 고양이 양육 가능 여부] 등의 feature가 있다 가정하자.
- ‘고양이 양육 가능 여부’의 집값에 대한 기여분을 제외하고, 그 외 모든 feature가 동일하다는 가정하에 310,000 (고양이 X) -320,000 (고양이 O) -10,000 으로 계산됨.
- 이러한 과정을 모든 가능한 조합에 대해 반복함.

- [숲세권, 면적, 층, 고양이 양육 가능 여부] = 4개
- 2^(4−1) = 8 개의 조합이 있고, 8개 각 조합에 대해 {f(조합1∪ 😺) - f(조합1)} + … + {f(조합8∪ 😺) - f(조합8)} 값을 산출하고, 이를 가중평균하여 ϕ(😺) 를 구함.
- ϕ(😺) 고양이 데이터에 대한 Shapley Value
2. SHAP
SHAP : Shapley Value 의 Conditional Expectation (조건부 기댓값)
Simplified Input을 정의하기 위해 정확한 f 값이 아닌, f 의 조건부 기댓값을 계산함.

- 오른쪽 화살표 (ϕ0,1,2,3) 는 원점으로 부터 f(x) 가 높은 예측 결과를 낼 수 있게 도움을 주는 요소
- 왼쪽 화살표 (ϕ4) 는 f(x) 예측에 방해가 되는 요소
SHAP은 Shapley Value (Local Explanation) 기반으로 하여, 데이터 셋의 전체적인 영역을 해석할 수 있음. (Global Surrogate)
모델 f 의 특징에 따라, 계산법을 달리하여 빠르게 처리함
- Kernel SHAP : Linear LIME, Shapley Value
- Tree SHAP : Tree based Model
- Deep SHAP : DeepLearning based Model
✔️ Global vs Local 대리 분석
Global Surrogate Analysis
학습 데이터(일부 또는 전체)를 사용해 대리 분석 모델을 구축하는 것
Local Surrogate Analysis
학습 데이터 하나를 해석화는 과정
Tree SHAP
Tree Ensemble Model 의 Feature Importance 는 모델(or 트리)마다 산출값이 달라지기 때문에, 일관성이 없다는 한계점이 존재함.

- Tree Model A와 B의 Feature는 Fever, Cough로 각각 동일하지만, Split 순서가 다른 것을 확인할 수 있음.
- Split 순서에 기반하여 계산되는 Gain, Split Count 등의 산출값이 달라지는 것을 확인할 수 있음.
- 즉, 같은 데이터로부터 학습이 된 모델이지만, 모델마다 Feature Importance가 달라지게 됨.
E[f(x)∣xS*] = *xS 가 속하는 Leaf node의 score 값 × 해당 node에 속하는 Training 데이터의 비중각 Tree 마다 Conditional Expectation E[f(x)∣xS] 를 구해, 다 더하여 최종 값을 산출함.
시간복잡도 : O(TLD2)T : 트리의 개수, L : 모든 트리의 최대 leaf 수, D : 모든 트리의 최대 깊이Kernel SHAP 에 비해 속도가 빠름.
따라서 SHAP은 Split 순서와 무관하게, 일관성있는 Feature Importance를 계산할 수 있음!
3. 시각화
Tree SHAP
# import packages
import pandas as pd
import numpy as np
from xgboost import XGBRegressor, plot_importance
from sklearn.model_selection import train_test_split
import shap
# load data
X, y = shap.datasets.boston()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=.2, random_state=1)
# modeling
model = XGBRegressor()
model.fit(X_train, y_train)SHAP value를 통해 Feature Attribution을 파악해보자.
# load js
shap.initjs()
explainer = shap.TreeExplainer(model)
shap_values = explainer.shap_values(X_train)Force_plot
특정 데이터 하나 & 전체 데이터에 대해, Shapley Value를 1차원 평면에 정렬해서 보여줌.

- 집 값 상승에 긍정적인 영향을 준 요인은 LSTAT (동네의 하위 계층 비율), 부정적인 영향을 준 요인은 RM (방의 수)가 집 값 형성에 부정적인 영향을 미쳤다고 해석할 수 있음

- DIS (주요 업무지까지 거리)가 가깝고, LSTAT (동네의 하위 계층 비율)이 적고, CRIM (범죄율)이 낮은 주택이 좋은 거주 환경 조건을 구성해 높은 집 값으로 형성되었다고 해석할 수 있음
Feature Importance
shap.summary_plot(shap_values, X_train, plot_type='bar')SHAP feature importance는 평균 절대 섀플리 값으로 측정되며 내림차순으로 정렬됨
전체 Feature가 Shapley Value 분포에 어떤 영향을 미치는지 Feature Importance 시각화를 할 수 있음.

summary_plot
shap.summary_plot(shap_values, X_train)summary_plot으로 feature와 예측에 미치는 영향 사이의 관계를 볼 수 있음.
하지만 정확한 관계를 확인하려면 shap 의존도 (SHAP Dependency plot)을 확인해야함.

위 시각화를 설명해보자면, LSTAT, DIS 가 낮을수록 집 값 상승에 좋은 영향을 미쳤음.
RM이 높을수록 집 값 상승에 좋은 영향을 미쳤음.
Dependence_plot
SHAP 특성 의존도는 가장 간단한 전역 해석도임. 1) 특성을 선택2) 각 데이터에서 인스턴스에 대해 X축에 특성값을 표시하고 Y축에 해당하는 섀플리 값을 사용하여 점을 표시
shap.initjs()
top_inds = np.argsort(-np.sum(np.abs(shap_values), 0)) # (13, ) : 각각의 Feature 에 대해 shap value 다 더한 것
# make SHAP plots of the three most important features
for i in range(2):
shap.dependence_plot(top_inds[i], shap_values, X_train)

영향력이 큰 변수들을 순서대로 출력하는 방법이며, top_inds[i]에 특정 Feature를 넣어 importance를 확인할 수 있음.
참조
'AI' 카테고리의 다른 글
| [tensorflow] TensorBoard 연동해서 학습률 확인하기 (0) | 2023.03.16 |
|---|---|
| [환경 설정] Tensorflow NVIDIA GPU 잡기, CUDA, cuDNN 설치 (0) | 2023.03.06 |
| 학사 졸업 💙 (2) | 2023.02.18 |
| [TimeSeries] 시계열 교차검증 with Python : TSCV (Time Serise Cross Validation) (0) | 2023.02.15 |
| [python] SHAP (SHapley Additive exPlanations), 설명 가능한 인공지능 (0) | 2023.02.09 |




