| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- ggplot2
- 소셜네트워크분석
- 다변량분석
- 빅분기
- Eda
- SQLD
- 에이블러
- dx
- 웹크롤링
- 하계인턴
- 에이블스쿨
- kaggle
- 딥러닝
- 시계열
- Ai
- 한국전자통신연구원 인턴
- httr
- python
- ML
- 빅데이터분석기사
- 시각화
- matplot
- 지도학습
- 한국전자통신연구원
- kt aivle school
- arima
- 가나다영
- SQL
- 하둡
- 머신러닝
- KT 에이블스쿨
- KT AIVLE
- 에트리 인턴
- 서평
- r
- 프로그래머스
- ETRI
- hadoop
- 기계학습
- cnn
- Today
- Total
소품집
[ML] Linear classification, regression (선형회귀) 본문
Linear Regression (선형회귀)
수식 미분으로 한 번에 구하는 방법

- sum of squared error를 최소화 하기 위해 미분하여 얻은 최소화 된 식은
- y = Xb (Xt)y = (Xt)Xb[(Xt)X]^(-1)(Xt)y = [(Xt)X]^(-1)(Xt)Xb [(Xt)X]^(-1)(Xt)y = b
- 즉, 주어진 데이터 (x,y)만 있으면 위 수식으로 한 번에 파라미터(beta값 ==기울기) 를 계산할 수 있음
- 계산이 끝나면, 그 파라메터로 테스트 데이터에 적용하여 예측값 ^y 생성이 가능함
Iterative(반복 수행) 방법으로 학습하는 방법
- 데이터 (각각 (x,y)값으로 취급)
- (2,5), (3,7), (4,9), (5,11)
- 선형 모델 가정하기: ax+by+c=0 (파라메터: a,b,c)
- a=1, b=1, c=-5로 가정
- → x+y-5=0
- 학습과정
- 위 데이터 4개를 대입
- 각 데이터의 x에 값을 넣으면, y^은 3,2,1,0 이 나옴
- Loss =(y-y^)^2, cost =mean-squared-error 라고 하면,
- Total-Loss = (5-3)^2+(7-2)^2+(9-1)^2+(11-0)^2 =214
- cost = 214/3 = 53.5
- Gradient Descent 적용하여, MSE가 가장 작은 파라메터 a,b,c를 찾아감
- → Least squares method
- 위 데이터 4개를 대입
Gradient Descent 기본개념 (참고)

- 예측치(가정)와 실제치의 차이 즉, 최저의 cost를 찾는 게 목표
- Gradient descent 알고리즘을 이용해 cost가 최저가 되는 점을 찾음
- Gradient descent 를 적용해 MSE가 가장 작은 파라메터 a,b,c를 찾음

- Gradient descent(경사 하강법)은 함수의 기울기(경사)를 구하여 기울기가 낮은 쪽으로 계속 이동시켜 이를 최소값이 나올 때 까지 반복시키는 것
- 위 식에서 알파는 학습률로 학습할 수록 갱신되는 보폭의 크기를 말함
- 알파가 너무 크면 최저점에 수렴하지 못할 확률이 크고 반대로 너무 작으면 시간소비와 오버피팅이 날 수 있음

i번째 데이터의 정답을 찾기 → 최소화 하기 위해 미분
즉, 오차값을 최소로 하는 파라메터 베타 값을 찾아가는 과정
Ridge, Lasso Regression
- Ridge regression : Linear regression에서 얻어지는 파라메터(weight=기울기)가 너무 커지지 않도록, L2 norm으로써 제한
- Lasso(Least Absolute Shrinkage and Selection Operator) regression : L1 norm으로 제한

!! 람다는 세기조건을 걸어주는 부분으로 파라메터 베타가 너무 커져 오버피팅을 막는 역할을 함

릿지에 비해 라쏘는 weigh 값을 0에 가깝게, 타이트 하게 잡는다. 릿지에 비교하여 더욱 작아지는건 릿지는 제곱, 라쏘는 절댓값을 cost함수에 각 각 곱하기 때문에상대적으로 값이 더 작게 나오는 라쏘의 파라메터 값 0에 가깝게 하지만 0이 아닌 정도로 감소 시킨다.
Linear Classification (Logistic Regression)
Regression vs Classification
regression은 real value를 예측하고 classification은 카테고리를 맞추는 문제 (True or false)
- 이름은 regression(회귀-최적의 기울기 값을 찾음)인데, 목적은 classification(분류)?
- 방법은 regression인데, 선형 합에 대하여 특별한 모종의 함수f를 채택함으로써, classification으로 적용됨
- 선형합 : ax+by+c
- 선형 합에 대하여 임의의 함수(f)를 적용하여 '확률값' 생성 → 의사결정이 가능해진다!
- ex) 확률값(0~1)으로 생성해주는 logistic function

그럼 왜 logistic function을 썼을까?
- 함수 f(x)의 결과값은 '확률'형태(0~1 사이), x값은 모든 숫자가 가능하도록 전환
- 즉 모든 값을 표현할 수 있되, 확률은 0~1 사이의 값이 되게 한다.
더 설명해보자면, 로지스틱 함수는 x값을 어떤 값이든 받을 수 있지만, 항상 출력 결과는 0~1에서 나온다.
즉 확률밀도 함수 요건을 만족시키는 함수가 된다!

++ 설명
(3) 승산(Odds)이란 임의의 사건 A가 발생하지 않을 확률대비 일어날 확률의 비율을 뜻하는 개념
(3) 만약 P(A)가 1에 가까울 수록 승산은 치솟을 겁니다. 반대로 P(A)가 0이라면 0이 될 겁니다. 바꿔 말하면 승산이 커질수록 사건 A가 발생할 확률이 커진다고 이해해도 될 겁니다. P(A)를 x축, 사건 A의 승산을 y축에 놓고 그래프를 그리면 아래와 같습니다.
예시!!


- 파라메터 최적화
- Gradient descent (경사 하강법)
- 위 cost function을 각 파라메터에 대해 편미분 하여, 각 파라미터를 그 값만큼 업뎃
- 학습이 끝난 Logistic regression 모델을 사용하여 분류하는 수식
- 모양새를 잘 보면, 아래 그림과 같이 decision boundary는 linear 하며, 선형 합이 0보다 큰지, 작은지에 의해 결정된다는 것을 알 수 있다.
- 선형합이 0 인것 == logistic function 값이 0.5인 것
- 모양새를 잘 보면, 아래 그림과 같이 decision boundary는 linear 하며, 선형 합이 0보다 큰지, 작은지에 의해 결정된다는 것을 알 수 있다.

(수정중)
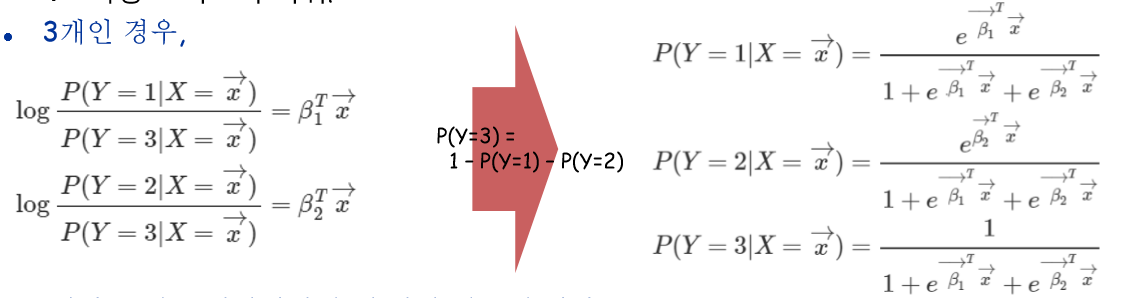
다항로지스틱 회귀
- 지금까지 본 것은 binary-case(label 두 가지)를 위한 Logistic regression

Classification vs Regression
Classification vs Regression
- Classification은 모델에 의해 예측하려는 '목적값'이 labeling 되어있음
- ex) 하마 vs 기린, 여자 or 남자
- Regression은 모델에 의해 예측하려는 '목적값'이 real-number
- ex) 사람의 몸무게, 나이, 키
- Classification과 Regression 둘 다, 지도학습(Supervised learning)에 속함
Linear Classification vs Linear Regression
- 둘 다 '선형 결합'에 의해 데이터를 모델링
- Linear classification은 0~1 사이의 확률값으로 결과값을 생성하여, threshold 값을 적용함으로써 '분류' 문제 해결 가능 ex) ) 선형합에 대한 threshold 로써 0사용
- Linear regression은 0~1 바깥의 값들이 나올 수 있으므로 확률값이 되지 못하므로 ;분류'문제에 해결이 부적합
참고
'AI' 카테고리의 다른 글
| [ML/DL] MLE, MAP (최대우도법, 최대사후법) (0) | 2020.05.06 |
|---|---|
| [ML/DL] PCA, SVD, Linear Discriminant Analysis (0) | 2020.05.01 |
| [ML/DL] Data mining introduction (0) | 2020.04.22 |
| [ML] Gaussian Naive Bayes와 Bayesian Networks (0) | 2020.04.15 |
| [ML] 나이브 베이즈 정리 (0) | 2020.04.12 |




