| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- ggplot2
- Ai
- 머신러닝
- python
- 기계학습
- 시각화
- 다변량분석
- 하계인턴
- KT AIVLE
- 하둡
- dx
- 에트리 인턴
- 서평
- 빅분기
- 빅데이터분석기사
- arima
- 에이블러
- r
- SQL
- 지도학습
- httr
- 프로그래머스
- matplot
- 웹크롤링
- Eda
- KT 에이블스쿨
- 한국전자통신연구원 인턴
- ML
- 소셜네트워크분석
- 에이블스쿨
- 시계열
- ETRI
- hadoop
- kt aivle school
- kaggle
- SQLD
- 딥러닝
- cnn
- 한국전자통신연구원
- 가나다영
- Today
- Total
소품집
[ML] Gaussian Naive Bayes와 Bayesian Networks 본문
2020/04/12 - [Data mining] - 나이브 베이즈 정리
앞의 포스팅과 이어집니다.
Gaussian Naive Bayes (가우시안 나이브 베이즈)

앞의 예시와 같이 베이즈안 분류와 나이브 베이즈 분류의 공통된 리스크는 학습 데이터가 없다면, 빈도수를 기반한 계산법이었기 때문에 0을 반환한다는 점이었습니다.
그래서 평균과 표준편차를 이용해 정규화된 모델인 가우시안 나이브 베이즈 모델을 정의할 수 있습니다.
GNB Classifier 학습
지금까지 P(x|class)를 단순히 빈도수에만 기반하여 학습 데이터가 없으면 0으로 나왔 던 리스크를 봐왔습니다. 그래서 이 리스크를 해결하기 위해 normalization 하여 가우시안 분포를 따른다고 가정하고, 문제를 풀어보려고 합니다.
우리는 가우시안 분포(사용하는 이유는 연속적 확률 분포로 널리 알려져있기 때문)를 가정해, 빈도수가 아닌 확률로 추정하는 방법을 택했는데요. 그래서 Feature에 대한 평균값과 표준편차를 계산해야 합니다.

k번째 레이블에 대해 얼마나 믿음직스러운가에 확률을 빈도수에 의해 측정하고,
모든 feature에 대해 평균과 SE를 계산합니다.

어떻게 계산할 수 있을까요. 먼저 GNB classifier 테스트를 확인합니다.
새로운 데이터 x를 class Y로 예측하는 과정에서 모든 피처에 대하여 곱해줍니다.
하지만 여기서도 0이나 올 수 있는 확률이 생기죠? 그래서 레이블이 k일 확률: prior(사전 확률)을 곱해줍니다. 이 값에서 최대 우도 함수가 되도록 가장 큰 값을 찾을 수 있게 되는 것입니다.
앞서 봤던 NB방식과 다른 점은 likelihood를 구할 때 GNB방식에서는 정규화를 거쳤다는 점입니다.
심화

Maximum Likelihood Estimates(MLE)
GNB classifier 학습 시, 파라미터 estimation 방법

i는 feature
k는 class(label)
δ: 예를 들어 두 개의 label이 있다고 하면 yk (k=0:salmon, k=1:sea bass)라 표현할 수 있습니다. 같으면 1, 다르면 0을 반환합니다.
- 평균값을 구할 때는 1/(k에 속하는 레이블의 개수)*(모든 레이블 k 중 i feature값을 all integral 한 값) 이 됩니다.
- 표준편차를 구할 때도 마찬가지입니다. 각각의 레이블과 feature에 대해 구한 평균치로부터의 거리를 구합니다. (거리니까 제곱)
Decision Boundary 예시

위의 GNB 학습을 거친 decision 바운더리
왼) wine Dataset
오) XOR toy Dataset
위 그림과 같이 확률분포 모양에 따라 바우너 리 모양이 바뀌는 것을 볼 수 있습니다.
하지만 오른쪽 XOR 데이터셋 그래프는 선형성을 찾아보기 어려운데요. 오른쪽 그래프를 3차원으로 표현하면 봉긋하게 솟은 모양(계란 노른자 처럼)으로 XOR 데이터 셋에 대하여 학습을 실패한 모습을 보여줍니다.
Bayesian Network
Bayesian Network : Belief network, Causal network 이라고도 불린다.
- Directed edges : direct dependence
- Absence of an edge : conditional indepndence
베이즈 네트워크(Bayesian network) 혹은 빌리프 네트워크(영어: belief network) 또는 방향성 비순환 그래픽 모델(영어: directed acyclic graphical model)은 랜덤 변수의 집합과 방향성 비순환 그래프를 통하여 그 집합을 조건부 독립으로 표현하는 확률의 그래픽 모델이다.
형식적으로, 베이즈 네트워크는 방향성 비순환 그래프로서, 그래프의 각 마디(node)는 변수를 나타내고, 마디를 연결하는 호(arc)는 변수 간의 조건부 의존성(conditional dependency)을 표현한다. 마디는 측정된 모수, 잠재 변수, 가설 등 어떤 종류의 변수든 표현할 수 있다. (source: 위키백과)
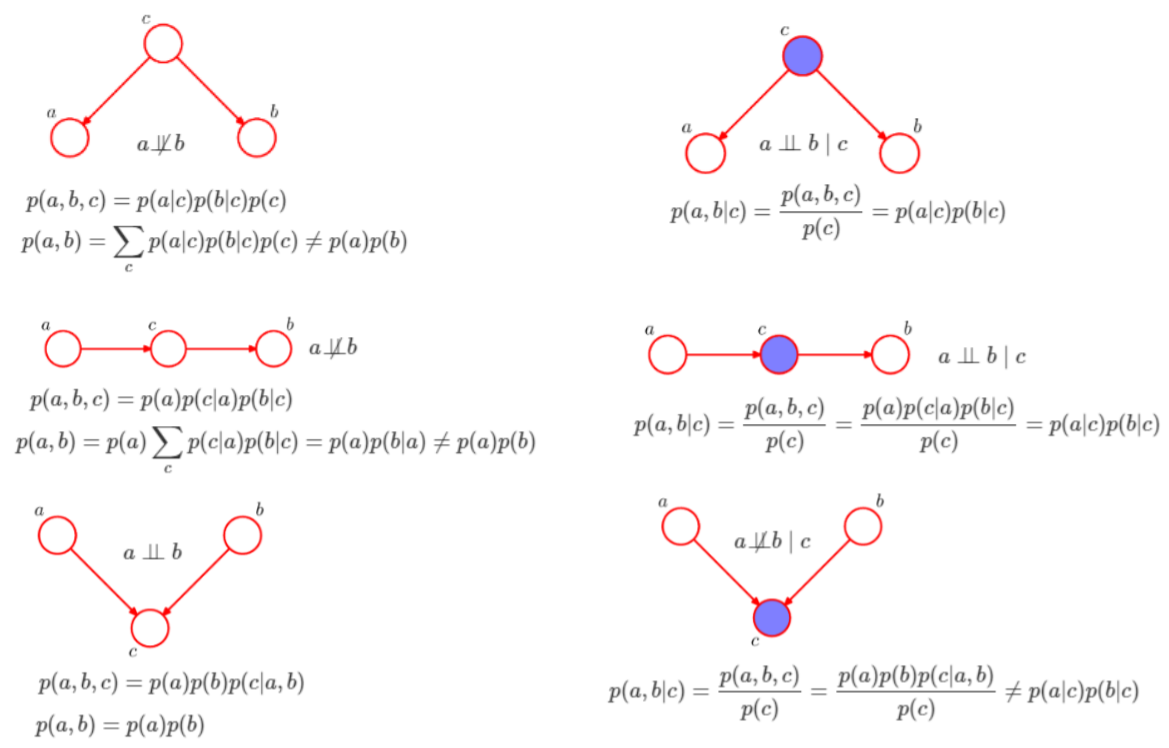
그림을 보면서 이해해 봅시다.
1 4
2 5
3 6
크게 왼/오른쪽을 나누어 보면 가장 큰 차이점은 보라색 원이 있냐 없냐 일 텐데요. 보라색 원은 '이미 결정된 주어진 값'입니다. 순서대로 6개의 network를 보면 이렇게 설명할 수 있습니다.
- c는 주어지지 않은 상태로 a와 b는 독립적이지 않고 c의 값에 따라 달라집니다. 그래서 a와 b는 독립이 아니라 할 수 있습니다.
- a는 c에 영향을 미치고, 다시 c는 b에 영향을 줍니다. 이 또한 a와 b는 독립적인 관계라 할 수 없습니다.
- a와 b가 동시에 c에 영향을 줄 수 있습니다. 하지만 c는 결정값이 존재하지 않으므로 a와 b는 서로간에 독립적으로 결정될 수 있습니다.
- c는 결정값으로 존재하므로, a와 b는 c로부터 받는 영향은 이미 결정되어 있습니다. 따라서 a와 b는 독립입니다.
- 정해진 값 c가 존재합니다. a가 c에 미치는 영향은 b에 영향을 주지 않기 때문에 a와 b는 독립이라 할 수있습니다.
- a와 b가 동시에 c의 결정값에 영향을 줬으므로, 둘은 독립이 아닙니다.



6번을 예시로 들어 설명해 보겠습니다.
잔디가 젖었다(결정된 값이라 가정)는 1)비가 왔다. 2) 스프링쿨러가 작동됐다로 예측할 수 있습니다. 하지만 이 둘은 동시에 일어날 확률이 낮죠. 그래서 예시 1)과 2)가 서로 ex)를 설명하기 위해 애쓰는 상황이 발생하게 되는 거에요.

아래와 같이 5개의 binary variable들이 있다고 가정해봅시다.
B = a burglary occurs at your house
E = an earthquake occurs at your house
A = the alarm goes off
J = John calls to report the alarm
M = Mary calls to report the alarm
Q. P(B|M,J)는 어떤 의미일까?
아래와 같이 Bayesian Network를 설계했다고 하자
P(J,M,A,E,B) = P(J,M|A,E,B)P(A|E,B)P(E,B)
~ P(J,M|A) P(A|E,B)P(E)P(B)
~P(J|A)(M|A)P(A|E,B)P(E)P(B) 로 설명할 수 있다.
Q. (.J,M,A,E,B) = P(J | A) P(M | A) P(A| E, B) P(E) P(B) 결과값을 계산하기 위해 필요한 확률값 개수는 몇개인가?
- 힌트 : P(J|A)에서는 2개
- 정답! 총 10개가 된다.
- 학습 데이터로부터 계산에 필요한 확률값들을 얻어내고, 추후 이를 사용하여 새로운 데이터에 대한 확률 계산에 이용 ex: 데이터로부터 각 확률값을 얻어 낸 후, P(John Calls|B,E) 게산에 이용
Bayesian Network for Classification
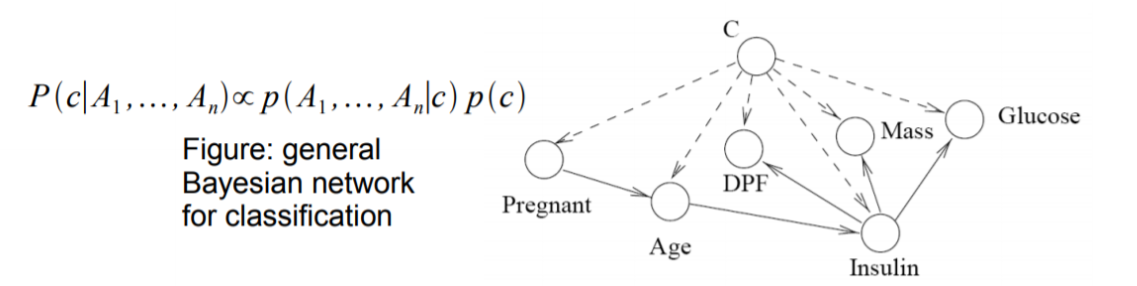
베이지안 네트워크는 분류 문제도 해결할 수 있습니다.
가장 상단 노드에 위치한 class C와 각 feature 간의 임의의 edge가 있습니다.
베이지안 네트워크의 각 노드들의 확률(빈도수를 기반으로) 세운 뒤, 완성된 베이지안 네트워크를 이용하여 새로운 데이터 X를 분류합니다.
이 때 각 class label에 대한 베이지안 확률은 posterior를 likelihood와 prior를 활용(이때, posterior는 likelihood와 prior를 곱의 비례한 값) 해 계산하여 곱해주고, 결과값으로 가장 큰 확률값의 label을 선택하게 됩니다.
- Class C와 각 feature 간의 임의의 edge
- 물론, feature 사이에도edge 가능
- Bayesian Network의 가가 노드들의 probability 완성
- Frequency 기반
- 물론, 별도의 probability distribution을 둘 수도 있음
- 완성된 Bayesian Network를 사용하여 새로운 데이터 X를'분류'
- 각 Class label에 대한 posterior probability 계산
- 가장 큰 확률값의 label을 선택하게 된다.

이 두개의 조건으로 나이브 베이즈 분류기는 그래프를 그려집니다.
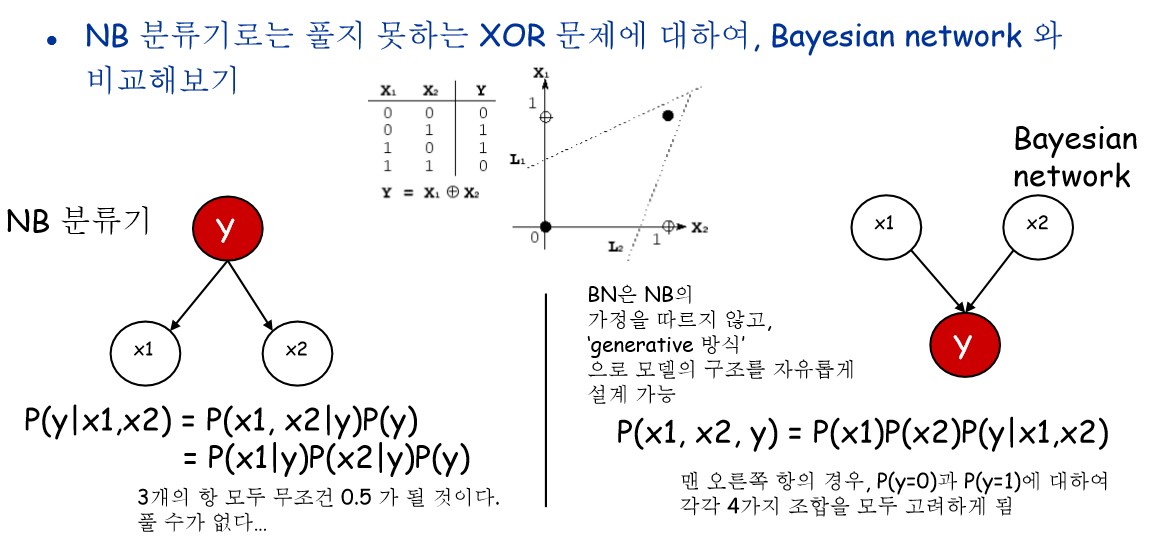
Bayesian Network for Classification

P(x1, x2|y) = P(x1|y)P(x2|y) 이 수식은 정당화 될 수 있을까요? 답은 안 됩니다.
좌변항의 경우에는 정해진 y가 x1과 x2를 결정하고 있습니다. 하지만 우변항은 feature 각각을 독립이라 가정하고 있기 때문에 수식은 성립되지 않습니다. 위에서 봐왔던 6번 예시를 설명하는데 뒷받침되죠.
[참고] Classification 종류
지금까지는 NB 문제에서 고려했던 문제는 Classification
Binary classification {salmon, sea bass}
Classification 종류
- Multi-class classification
- ex : {사자, 기린, 하마} 중에 맞추기
- 즉, 각 데이터는 단 1개의 class만 가능
- Multi-label classification
- ex) {모자, 스카프, 선글라스} 중에 맞추기
- 즉, 동시에 여러개의 class에 대한 label을 가질 수 있다.
참조
By Alisneaky, svg version by User:Zirguezi - 자작, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=47868867
https://www.quora.com/What-is-the-decision-boundary-for-Naive-Bayes
https://hwiyong.tistory.com/27
'AI' 카테고리의 다른 글
| [ML/DL] PCA, SVD, Linear Discriminant Analysis (0) | 2020.05.01 |
|---|---|
| [ML] Linear classification, regression (선형회귀) (0) | 2020.04.23 |
| [ML/DL] Data mining introduction (0) | 2020.04.22 |
| [ML] 나이브 베이즈 정리 (0) | 2020.04.12 |
| [ML] Decision Tree (의사결정 나무) (0) | 2020.04.04 |




