| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- SQL
- kaggle
- dx
- 프로그래머스
- 빅데이터분석기사
- 웹크롤링
- KT AIVLE
- python
- hadoop
- KT 에이블스쿨
- kt aivle school
- 빅분기
- matplot
- 에트리 인턴
- 머신러닝
- 한국전자통신연구원 인턴
- 한국전자통신연구원
- httr
- ETRI
- 에이블스쿨
- 딥러닝
- r
- Eda
- 에이블러
- Ai
- 시각화
- 기계학습
- cnn
- 하둡
- ggplot2
- 서평
- 가나다영
- 시계열
- arima
- 소셜네트워크분석
- SQLD
- ML
- 지도학습
- 하계인턴
- 다변량분석
Archives
- Today
- Total
소품집
[ML/DL] SVM (Support Vector Machine) 본문
728x90
SVM: Motivation
(+)와 (-)의 class를 구분짓기 위해서는 여러 방법을 생각할 수 있습니다.
그러면 어떻게 나눠야 잘 나눴다고 할 수 있을까요?

아마 제일 잘 나눴다고 볼 수 있는 형태는 이런 모습일 것 입니다.


나누는 목적: 데이터 클래스 (class, label) 분류
- 그렇다면, '잘 나눈다'는 것 == 클래스 사이의 딱 중간이 아닐까?
- 딱 중간 이라면, 서로 다른 클래스 간에 **'거리가 최대'**가 되게 하는 것
- 정리해보면, SVM에서 찾고자 하는 decision boundary 는 다른 클래스에 속한 데이터들 간에 '거리가 최대'가 되게 하는 boundary라 볼 수 있게 되고,이 때 boundary를 **'Max margin'**이라 합니다.
- 이 boundary는 두 개의 경계(노란선)의 중간선이 되며, 유일한 두 개의 경계선을 만족하려면 최소 2개(feature 개수 상관없이)이 데이터가 노란선 위에 위치해야 합니다.
- → 이 데이터(벡터)들을 Support Vector라고 함
- Decision boundary를 표현하는 수식
- W(방향벡터)•x+b=0
- Decision boundary에 정확히 위치한 데이터를 위 수식에 적용하면 만족하게 됨
- W(방향벡터)•x+b=0

SVM: Motivation
Decision Boundary가 되려면?
- W^T•X+b=0의 수식을 따르는 선형을 Decision Boundary라고 함
- 또한 가중치 벡터 W는 Decision Boundary와 직교(=90도)해야 한다.
왜 W와 Decision Boundary는 직교해야 하는가?
- 계산상 편의를 위해, b=0(원점을 지남)로 가정하면,
- W^TㅁX=0 → Decision Boundary로 정의할 수 있게 됨
- 2개 벡터 내적의 결과가 0이 되는 각도는 90도 이므로 직교한다고 표현!!
왜 벡터 내적의 합이 0이면 90도가 되는가?
- 2개 벡터(W,X)의 내적은 P
- 이때 내적의 값이 가장 커지는 각도는 0도가 되고, 내적의 값이 0이 되는 각도는 90도가 된다.
- 즉, W•X=0일 때, 벡터 X의 모든 점들은 벡터 W에 직교한다는 의미가 됨

Small Margin vs. Large Margin

또한 class간의 분류를 더 잘 하기 위해서는 class간의Margin이 최대가 되어야 합니다.
즉, Max-margin은 유일해야 합니다.
→ 그렇게에, 아래 그림과 같이 최소 2개의 Support Vector가 필요 (여기선 총 3개 존재)
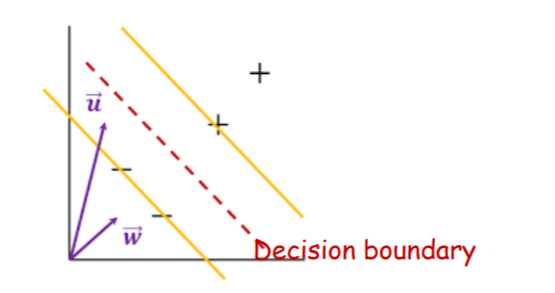
SVM 분류 방법
- Decision boundary에 데이터를 적용한 '부호' 판별
- 임의의 데이터 u(방향벡터)를 Decision boundary 수식에 적용하면,
- w•u+b < 0 이므로, '-' 클래스로 분류
- 또는, Boundary까지의 거리 개념을 도입함
- u를 w에 projection(정사영)한 뒤, 그 길이가 boundary 까지 닿느냐 안닿느냐?를 확인해 보는 과정
- 좀 더 Formal 하게 정리해보면, boundary와 노란색 선까지의 거리를 1이라고 가정하여,
- w•x+b ≤ -1
- w•x+b ≥ 1
잘 분류해낼 수 있는 SVM을 얻기 위해서는 데이터를 기반으로 학습과정을 겨쳐 w와 b를 계산해야함
수식에 앞서
Normal Vector (법선 벡터)

Distance (거리)

Lagrange Multiplier 예시


수식으로 보는 SVM




비선형 패턴을 위한 SVM
- Decision boundary 양 옆의 경계선을 침범하여 일부 틀린 데이터들에 대하여 대충 넘어가주기 위한 변수
- Slack variable을 추가함으로써 최적화 문제를 풀기 어려워짐


- 변수 C(hyper parameter): 오분류되었지만 대충 넘어가주는 것에 대한 비용
- C를 크게 할수록 대충 넘어가기 어려워지므로, 정확히 분류해내도록 학습(Overfitting유도)
- C를 작게 할수록 대충 넘어가기 쉬워지므로, 정확하지 않게 분류해내도록 학습
Kernel trick
- 선형 판별이 안 되는 경우에 대하여, 선형 판별 되는 공간으로 변경하기 위해 kernel 함수 적용

728x90
'AI' 카테고리의 다른 글
| [ML] Hierarchical Clustering - 계층적 군집 (0) | 2020.06.13 |
|---|---|
| [ML] Semi-Supervised Learning, K-means clustering (0) | 2020.06.13 |
| [ML/DL] ANN 학습: Back-propagation (역전파 알고리즘 ) (0) | 2020.05.28 |
| [ML/DL] Artificial Neural Network (인공신경망) (0) | 2020.05.11 |
| [ML/DL] Perceptron (퍼셉트론) (0) | 2020.05.11 |
Comments




