| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- 하둡
- 빅데이터분석기사
- 다변량분석
- 지도학습
- 기계학습
- 한국전자통신연구원 인턴
- 빅분기
- ML
- 시각화
- 에트리 인턴
- 가나다영
- 프로그래머스
- httr
- hadoop
- SQLD
- Ai
- KT AIVLE
- 딥러닝
- 한국전자통신연구원
- matplot
- kaggle
- 하계인턴
- r
- ggplot2
- python
- 소셜네트워크분석
- ETRI
- KT 에이블스쿨
- 머신러닝
- cnn
- 서평
- 에이블스쿨
- SQL
- dx
- 시계열
- 에이블러
- Eda
- arima
- kt aivle school
- 웹크롤링
- Today
- Total
소품집
이동평균모형 (Moving average models : MA) 식별법 본문
2020/06/12 - [time series] - 자기회귀모형 (Autoregressive models : AR) 식별법
자기회귀모형 (Autoregressive models : AR) 식별법
정의 AR (Autoregressive model) : 시계열 yt를 종속변수로 그 이전 시점의 시계열 yt-1, … , yt-p 독립변수로 갖는 회귀모형의 형태 𝜀𝑡 normally distributed white noise (평균 = 0, 분산 = 1)으로 가정 즉..
sodayeong.tistory.com
이전글과 이어집니다.
모형식별(correlogram 활용법)

이동평균모형 (Moving average models : MA)
정의
- 시점 t의 y는 예측오차 (forecast errors)의 가중이동평균으로 표현

- 𝜀𝑡 normally distributed white noise (평균 = 0, 분산 = 1)으로 가정
- C는 drift term(절편)을 의미 (상수 = 평균!)
- q 차 이동평균모형이라 하며 MA(q)로 표시
- 보통 q=1 또는 q=2 까지 영향을 미치며, 이를 MA(1), MA(2) 모형이라 함
- 이동평균평활법과(Moving average smoothing)는 다른모형
- MA(1)와 MA(2) 모형

MA(q)모형

MA(1) 모형 시뮬레이션
데이터 생성 방법 (MA(1))
set.seed(12)
y <- ts(numeric(300))
e <- rnorm(300) #백색잡음
for(t in 2:300){
y[t] <- 𝜃 * e[t-1] + e[t]
}
# 2가지 확인 사항
ggtsdisplay(y)
Arima(y, order=c(0,0,1)) #계수(모수) 추정값 확인하기
arima.sim() 함수를 이용한 ARIMA 모형 데이터 생성
# AR 모형 생성
AR_1 <- arima.sim(list(order=c(1,0,0),ar=0.7),n=300)
AR_2 <- arima.sim(list(order=c(2,0,0),ar=c(0.3,0.2)),n=300)
# MA 모형 생성
MA_1 <- arima.sim(list(order=c(0,0,1),ma=0.8),n=300)
MA_2 <- arima.sim(list(order=c(0,0,2),ma=c(0.8,0.3)),n=300)
arima.sim() 함수를 이용한 ARIMA 모형 데이터 생성 방법
- 정상성, 가역성 조건에 맞지 않는 계수값들을 대합하면?
- 에러가 발생한다. (단, AR의 경우에만 에러가 발생)
- MA 모형은 항상 정상성을 만족하기 때문에 에러가 발생하지 않음 (주의 해야함.)
- 에러가 발생한다. (단, AR의 경우에만 에러가 발생)

Φ(계수 값)에 따른MA(1) 데이터 시뮬레이션
Φ1=0.9 인 경우
MA_1 <- arima.sim(list(order=c(0,0,1),ma=0.9),n=300) # 데이터 생성
ggtsdisplay(MA_1)
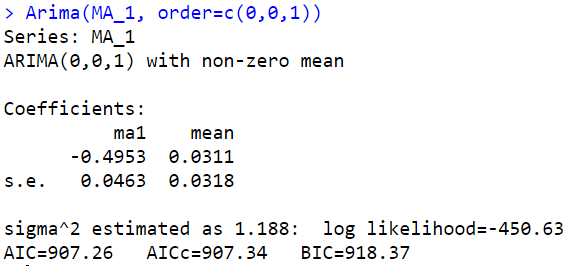
Arima(MA_1, order=c(0,0,1))


Φ1=0.6 인 경우
MA_1 <- arima.sim(list(order=c(0,0,1),ma=Φ1),n=300) # 데이터 생성
ggtsdisplay(MA_1)
Arima(MA_1, order=c(0,0,1))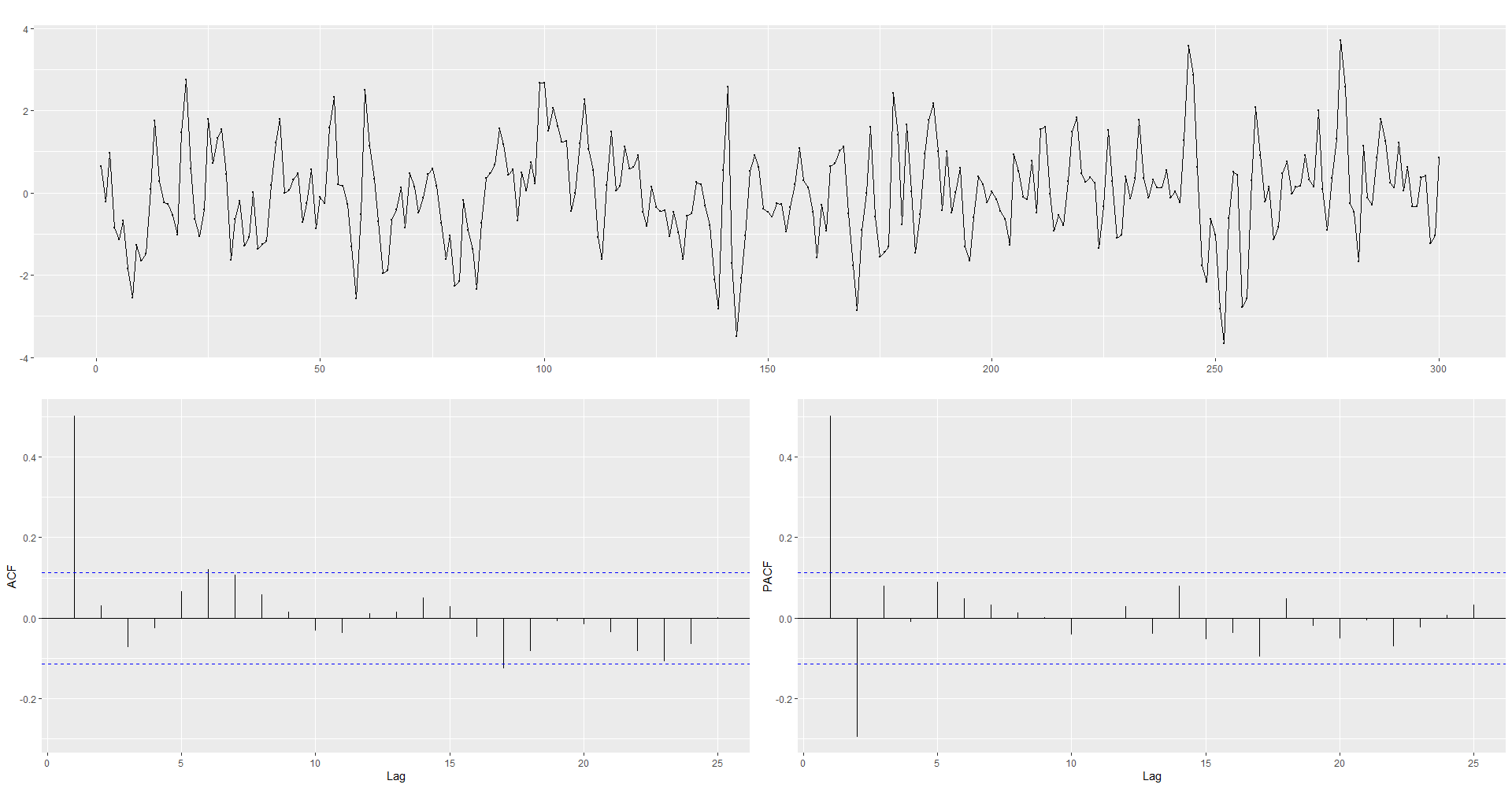

Φ1=-0.8 인 경우


Φ1=-0.5 인 경우

MA(2) 모형 시뮬레이션
Φ1=0.8, Φ2=0.3 인 경우
MA_2 <- arima.sim(list(order=c(0,0,2),ma=c(Φ1,Φ2)),n=300)
ggtsdisplay(MA_2)
Arima(MA_2, order=c(0,0,1))

가상의 MA(2) 시계열로 분석해보기 (Box-Jenkins 방법론)
# 𝜃1 (계수 값) = 0.6인 MA(1)시계열 생성
set.seed(12)
MA_1 <- arima.sim(list(order=c(0,0,1), ma=0.6),n=300) # 데이터 생성
# 데이터 나누기
train <- window(MA_1, start=1, end=250)
test <- window(MA_1, start=250, end=300)
모형식별
ACF와 PACF를 통해 모형식별
# ACF와 PACF를 통해 모형 식별
ggtsdisplay(train) # ACF는 MA(1)을 보이는 반면 PACF는 MA(2)로 파악된다.
H0 : 정상시계열
H1 : 정상시계열이 아니다
통계검정 활용 - KPSS 검정
유의수준 0.01에서 임계값 0.739일 때 검정통계량은 0.048이 나왔습니다. 유의수준 안에 검정통계량이 속하므로 귀무가설을 채택하게 됩니다. 즉 정상시계열을 만족한다.

모수 추정
Arima() 함수 이용 (log MLE 방법이 default로 들어가 있음!)
- Train set을 모수추정 시행
- ARIMA 모형에서 order=c(0,0,1) 할당
# MA(1)인 경우
Arima(train, order=c(0,0,1))
Arima(train,order=c(0,0,1), include.mean = F) # 절편이 없는 모형
auto.arima(train) # 정보손실을 바탕으로 가장 우수한 걸 뽑아 보여줌
또한 MA(q) 모형의 식으로 표현해보면 아래와 같이 나타낼 수 있습니다.
𝑦=0.5464𝑦𝑡−1+ε𝑡−0.0151 (mean) 𝑦=0.5465𝑦𝑡−1+ε 𝑡 𝑦=0.5465𝑦𝑡−1+ε 𝑡
적합성 진단 (Diagnosis)
통계 검정을 통해 모형 선정 (잔차의 독립성 확인 및 검정)
- 잔차 독립성 검정 후, 적합하지 않은 경우 모형 추정
- chekresiduals() 함수 이용하여 잔차 ACF와 잔차 분포 확인
- Ljung-Box 검정을 통한 잔차 확인 (포트맨토 검정)
MA_1_fit <- Arima(train, order=c(0,0,1))
checkresiduals(MA_1_fit)
MA_1_fit_meanf <- meanf(train,h=50)
checkresiduals(MA_1_fit_meanf)
MA_1_fit_naive <- naive(train, h=50)
checkresiduals(MA_1_fit_naive)





예측
MA_1_F <- forecast(MA_1_fit, h=50)
MA_1_F_meanf <- meanf(train, h=50)
MA_1_F_naive <- naive(train, h=50)
accuracy(MA_1_F, test)
accuracy(MA_1_F_meanf, test)
accuracy(MA_1_F_naive, test)
- Train set에 대하여 test set의 accuracy를 파악해본 결과 train과 test의 차이가 가장 작은 MA(1) 모형이 가장 잘 적합 된 것으로 보입니다.
- 과적합된 모델은 없는 것으로 보입니다.
적합 및 예측 값 차트로 표현하기
MA(1) forecast

meanf

평균에 적합되었습니다.
naive

실제 값과 적합된 값에서 약간 오른쪽으로 한 칸씩 밀려진 모습을 모여줍니다. 실제값과 적합값의 차이가 적은 것으로 보여집니다.
'Time series' 카테고리의 다른 글
| ARMA model - 자기회귀이동평균 (0) | 2020.06.22 |
|---|---|
| ARMA model (0) | 2020.06.20 |
| 자기회귀모형 (Autoregressive models : AR) 식별법 (0) | 2020.06.12 |
| KPSS 검정 (0) | 2020.06.08 |
| ARIMA model & 정상성 파악 (0) | 2020.06.05 |


