| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- 시계열
- 프로그래머스
- SQL
- r
- 소셜네트워크분석
- 서평
- matplot
- 에이블스쿨
- 에트리 인턴
- kaggle
- 하계인턴
- 시각화
- SQLD
- 에이블러
- ML
- ggplot2
- hadoop
- 머신러닝
- arima
- 다변량분석
- KT 에이블스쿨
- ETRI
- 기계학습
- kt aivle school
- dx
- 딥러닝
- 한국전자통신연구원 인턴
- 지도학습
- httr
- 웹크롤링
- python
- Eda
- 하둡
- 빅데이터분석기사
- 가나다영
- 빅분기
- 한국전자통신연구원
- KT AIVLE
- Ai
- cnn
- Today
- Total
소품집
ARMA model - 자기회귀이동평균 본문
13장 (ARMA model)
Backward shift operator, 후진 연산자(B)
시계열 데이터의 래그(lag,L = 이전 시점 데이터)값을 표현

ARMA
자기회귀이동평균 (AR+MA)

위 식을 전개하기 전의 식은 yt=AR(p)+MA(q)로 쓸 수 있게 된다.

- ARMA(p,q) 모형은 AR(p) 모형과 MA(q) 모형의 특징을 모두 가지는 모형을 말한다. 즉 p개의 자기 자신의 과거값과 q개의 과거 백색 잡음의 선형 조합으로 현재의 값이 정해지는 모형이다.
- Yt=−ϕ1Yt−1−ϕ2Yt−2−⋯−ϕpYt−p+ϵt+θ1ϵt−1+θ2ϵt−2⋯+θqϵt−q
- 제약조건은 이 둘의 조건을 모두 만족해야하며, 모수 값을 적게 가져가는 모델을 더 높히 평가하는 추세임.
ARMA 모형 시뮬레이션
ARMA(1,1) 모형
- ARMA(1,1) 모형 (Φ1 > 0, 𝜃1< 0)
- ARMA(1,1) 모형 (Φ1 > 0, 𝜃1> 0)
- ARMA(1,1) 모형 (Φ1 < 0, 𝜃1< 0)
- ARMA(1,1) 모형 (Φ1 < 0, 𝜃1> 0)
ARMA(2,1) 모형
ARMA(1,2) 모형
ARMA(2,2) 모형
데이터 시뮬레이션을 통해 각 ACF와 PACF의 패턴을 확인
- 추가적으로 auto.arima()와 Arima() 함수를 사용하여 모형 추정
- 주의> auto.arima() 남용하지말 것
- auto.arima() 함수 이용시 mean 값을 포함하는 경우 → AICc값을 개선하는 경우가 된다.
- 또한 -1<Φ<1 일 때, 0.99, 0.9, 0.8 등등 다양하게 생성시켜 비교해보기.
ARMA 모형 시뮬레이션
AR(1,1) 모형 (Φ1 > 0, 𝜃1 < 0)
# ARMA(1,1) 모형(Φ1 > 0, 𝜃1 < 0)
set.seed(1234)
arma_1_1 <- arima.sim(model=list(order=c(1,0,1),ar=0.7,ma=-0.2),n=200)
ggtsdisplay(arma_1_1)
Arima(arma_1_1,order=c(1,0,1))
auto.arima(arma_1_1)

ARMA(1,1) 모형 (Φ1 > 0, 𝜃1> 0)
set.seed(1234)
arma_1_1 <- arima.sim(model=list(order=c(1,0,1),ar=0.7,ma=0.2),n=200)
ggtsdisplay(arma_1_1)
Arima(arma_1_1,order=c(1,0,1))
auto.arima(arma_1_1)



ARMA(1,1) 모형(Φ1 < 0, 𝜃1< 0)
# ARMA(1,1) 모형 (Φ1 < 0, 𝜃1 < 0)
set.seed(1234)
arma_1_1 <- arima.sim(model=list(order=c(1,0,1),ar=-0.7,ma=-0.2),n=200)
ggtsdisplay(arma_1_1)
Arima(arma_1_1,order=c(1,0,1))
auto.arima(arma_1_1)

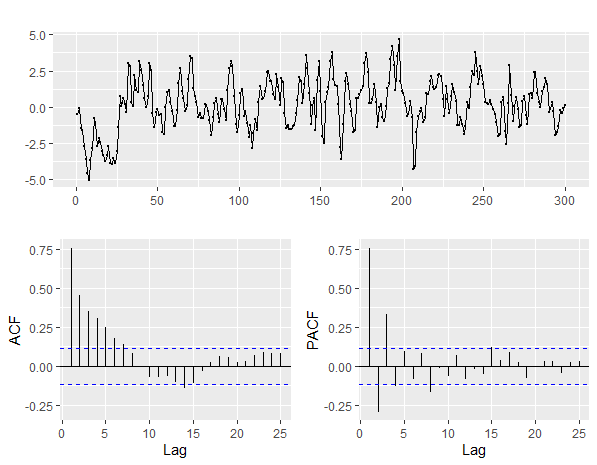

ARMA(1,1)모형 (Φ1 < 0, 𝜃1> 0)
set.seed(1234)
arma_1_1 <- arima.sim(model=list(order=c(1,0,1),ar=-0.7,ma=0.2),n=200)
ggtsdisplay(arma_1_1)
Arima(arma_1_1,order=c(1,0,1)) # include.mean=FALSE 설정시 auto.arima함수와 동일 값 반환!
auto.arima(arma_1_1)

ARMA(2,1) 모형
# AR(2,1) 모형
set.seed(1234)
arma_2_1 <- arima.sim(model=list(order=c(2,0,1),ar=c(0.7,-0.6),ma=-0.4),n=300)
ggtsdisplay(arma_2_1)
Arima(arma_2_1,order=c(2,0,1))
auto.arima(arma_2_1)

auto.arima()의 남용하지 말아하는 이유는, 기존 Arima()를 사용했을 때 보다 AICc 값이 더 크게 나오는 경우도 있기 때문이다.
ARMA(1,2) 모형
# AR(1,2) 모형
set.seed(1234)
arma_1_2 <- arima.sim(model=list(order=c(1,0,2),ar=0.8,ma=c(0.3,-0.5)),n=300)
ggtsdisplay(arma_1_2)
Arima(arma_1_2,order=c(1,0,2))
auto.arima(arma_1_2)

ARMA(2,2)모형
set.seed(1234)
arma_2_2 <- arima.sim(model=list(order=c(2,0,2), ar=c(0.7,-0.6), ma=c(0.3,-0.5)),n=300)
ggtsdisplay(arma_2_2)
Arima(arma_2_2,order=c(2,0,2))
auto.arima(arma_2_2)


ARMA 모형의 ACF 및 PACF
요약

참고사항 (ARMA 모형)
- 시차 K > q-p 에서, 자기상관함수(ACF)는 자기회귀모형(AR)의 자기상관함수의 지수적으로 감소하는 모습을 보임
- 시차 K > q-p 에서, 편자기상관함수(PACF)는 이동평균모형(MA모형)의 편자기상관함수의 형태인 지수적으로 감소하는 모습을 보임
- 자기상관함수(ACF)와 편자기상관함수(PACF)는 시차 K가 커짐에 따라 각각 감소하는 형태를 보임
예제
Data
- uschange Data (fpp2 packages)
- US consumption expenditure
library(fpp2)
autoplot(uschange[,'Consumption']) +
xlab('Year') + ylab('Quarterly percetage'
정상성 확인

library(fpp2)
autoplot(uschange[,'Consumption']) +
xlab('Year') + ylab('Quarterly percetage')
ggtsdisplay(uschange[,'Consumption'])H0 : 정상시계열이다
H1 : 정상시계열이 아니다
유의수준 1%

유의수준 0.01에서 임계값 0.739로 관측되었고, 이 때의 검정통계량은 0.2848로 관측되었습니다.
검정통계량은 유의수준 안에 들어오므로 귀무가설을 채택합니다.
즉, 정상시계열을 만족합니다.
모형 적합1 (auto.arima함수)
- Auto.arima를 통해 적합 (non-seasonal ARIMA 사용)

모형 적합2 (Arima 함수)
- 차수를 어떻게 정해햐 할지는 분석자가 결정해햐할 hyper parameter임
- Arima(uschage[,'Consumption'], order=c(?,0,?)) → 여기서 적절한 p, q 값은?
모형적합 1 (auto.arima 사용)
-
auto.arima를 통해 적합 (non-seasonal ARIMA 사용)
→ 위의 식에서 sigma^2의 값은 0.3499
-
ARIMA(1,0,3)으로 모형 적합

- C = 0.7454*(1-0.589) = 0.307
- 𝜀t (백색잡음) → 표준편차가 0.592 = sqrt(0.350)
모형 적합2 (Arima 함수로 적합)
- 차수를 어떻게 정해야 할까?
- Arima(uschange[,'Consumption'],order=c(?,0,?))

**ggAacf(uschange[,'Consumption'])**
**ggPacf(uschange[,'Consumption'])**
비교
summary(적합모형)
- 여기서 fit 변수는 auto.arima, fit_1은 Arima(3,0,0) 적합모형을 뜻함


두 모델의 성능을 비교하고자 AICc와 RMSE를 기준삼아 평가해보겠습니다.
- 먼저 auto arima를 사용한 fit의 summary의 AICc는 후자 Arima(3,0,0) 모델보다 높게 나왔습니다.
auto.arima가 항상 좋은 평가만 내지 않는 다는 것을 확인할 수 있는 예제가 됩니다.
- 다음으로는 RMSE(Roort mean squre error)입니다. 실제 오차값과 차이가 적을수록 좋은 모델로 평가됩니다. 여기서는 auto.arima()를 이용한 fit이 에러가 더 작게 나왔습니다.
잔차 확인
여기서 fit 변수는 auto.arima, fit_1은 Arima(3,0,0) 적합 모델임.
checkresiduals(fit) # auto.arima는 ARIMA(1,0,3)으로 예측
checkresiduals(fit_1) # Arima()는 ARIMA(3,0,3)으로 적합

Source
https://otexts.com/fppkr/arima-estimation.html
https://datascienceschool.net/view-notebook/9cbbfed6d6f34f02a2cdaa422706be91/
'Time series' 카테고리의 다른 글
| 시계열 분해 알고리즘 - LOESS (MSTL) (0) | 2023.12.15 |
|---|---|
| ARIMA models (0) | 2020.06.22 |
| ARMA model (0) | 2020.06.20 |
| 이동평균모형 (Moving average models : MA) 식별법 (0) | 2020.06.12 |
| 자기회귀모형 (Autoregressive models : AR) 식별법 (0) | 2020.06.12 |



