| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- 에이블스쿨
- 기계학습
- 한국전자통신연구원
- 시계열
- KT AIVLE
- ggplot2
- arima
- SQL
- 하계인턴
- ML
- r
- 빅데이터분석기사
- matplot
- python
- 소셜네트워크분석
- ETRI
- 지도학습
- hadoop
- 머신러닝
- 빅분기
- 시각화
- 다변량분석
- 서평
- 에트리 인턴
- Eda
- kt aivle school
- 하둡
- Ai
- cnn
- 웹크롤링
- 한국전자통신연구원 인턴
- KT 에이블스쿨
- SQLD
- 딥러닝
- 에이블러
- dx
- 가나다영
- kaggle
- 프로그래머스
- httr
- Today
- Total
소품집
[다변량 분석] 모형 적합성, 회귀계수 유의성 검정, 결정계수(R^2) 해석 본문
1. 상관계수
공분산
- 두 확률 변수 사이의 관계를 선형관계로 나타낼 때 두 변수 사이의 상관 정도를 타나내며 다음과 같이 구합니다.
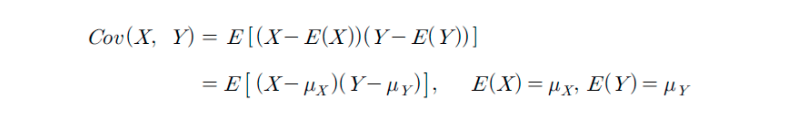
두 확률변수 X, Y의 공분산은 𝐶𝑜𝑣 (𝑋, 𝑌 )로 표기하며, 공분산이 갖는 값에 따라 두 확률변수의 관계를 파악할 수 있습니다.
- 𝐶𝑜𝑣 𝑋, 𝑌 > 0 : 두 확률변수 𝑋, 𝑌 의 변화가 같은 방향임을 나타냅니다. 즉 𝑋 증가하 면 𝑌 도 증가하고, 반대로 한 변수가 감소하면 같이 감소합니다.
- 𝐶𝑜𝑣 𝑋, 𝑌 < 0 : 두 확률변수 𝑋, 𝑌 의 변화가 다른 방향임을 나타냅니다. 즉 𝑋 증가하 면 𝑌 는 감소, 즉 한 변수가 감소하면 다른 변수는 증가합니다.
- 𝐶𝑜𝑣 𝑋, 𝑌 = 0 : 두 확률변수 간에 어떠한 (선형) 관계가 없음을 나타냅니다.
상관계수 [-1~1]

- 두 확률변수 𝑋, 𝑌의 공분산을 각 확률변수의 표준편차 곱으로 나눈 값을 상관계수라 하고, 기호로 𝜌𝑋𝑌 (혹은 𝜌)로 나타냅니다.

- 공분산의 경우 자료의 단위에 따라 값의 크기가 일정하지 않아 비교하기 힘듭니다.
- 공분산의 성질을 그대로 이어 받아 두 변수 간의 변화하는 방향이 같으면 양수, 그 반대이면 음수를 갖습니다.
- -1 혹은 1에 가까울수록 강한 상관을 나타내며, 0에 수렴할 수록 약한 상관을 나타냅니다.
2. 회귀분석
- 독립변수와 종속변수를 구별하고 인과관계에 대해 학습
- 통계적 모형 구축의 예로 단순선형회귀분석의 과정을 학습
- 회귀분석의 가정을 만족하는지 확인하는 방법에 대해 학습
인과관계
원인과 결과 관계를 뜻하는 인과관계는 상관관계처럼 계산을 통해 구하는 것이 아닌, 자료의 관찰로 파악이 가능한 관계입니다.
아래 도표를 봅시다.
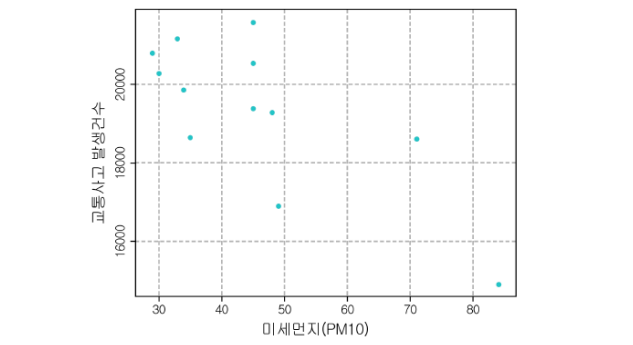
위 도표는 미세먼지(PM-10) 농도에 따라 교통사고 발생이 어떤 연관이 있는지 알아보고자 작성해본 도표입니다.
전반적으로 미세먼지 농도가 짙어질 수록 교통사고 발생은 줄어드는 경향을 보이고 있습니다.
이를 통해 미세먼지가 증가하면 교통사고 건수가 줄어든다고 할 수 있을까요?
아닙니다.
위 실험은 통제할 수 없는 요인(미세먼지)이기에 사전지식을 생각해보며 인과관계를 도출해야합니다.
따라서 다음을 같이 고민해봐야 합니다.
- 두 변수의 연관성
- 원인과 결과에 대한 고민
- 제 3의 요인
사례 (위키피디아 참조)
- 아이스크림 판매량이 증가할수록 익사사고 발생이 증가하였다. 즉 익사사고 발생을 억제하기 위해 아이스크림의 판매를 금지해야 한다(제3의 요인 : 계절).
- 불을 켜고 자는 어린이의 경우, 나이가 들어 근시가 될 경우가 많다. 즉 근시를 예방 하기 위해 어릴 때부터 잠을 잘 때 불을 켜지 말아야 한다(제3의 요인 : 부모의 근시).
- 국가 부채가 GDP의 90% 이상이 될 경우 국가의 성장률이 느려진다. 즉 높은 국가 부채는 국가의 성장을 느리게 한다(뒤바뀐 인과관계)
- 사과의 수입이 증가할수록 이혼률이 증가한다. 즉 이혼률을 낮추기 위해 사과 수입 을 금지한다(인과관계를 확인할 수 없는 두 변수)
2. 단순선형회귀분석
단순선형회귀모형
- 두 확률변수 X, Y에서 X가 독립변수이고, Y가 종속변수일 경우 독립변수 X의 개별값 X1, X2, ... , Xn에 대응하는 종속변수 Y의 관찰값 y1, y2, ..., yn에 대해 다음과 같은 모형을 단순선형회귀모형이라고 합니다.

회귀계수
- 위 식에서 두 상수 𝛽0, 𝛽1을 (모집단)회귀계수라 하는데, 이는 각각 직선의 방정식에서 절편과 기울기의 역할을 합니다.
- 두 상수는 미지의 모수로, 표본으로부터 추정을 통해 구합니다.
- 추정된 회귀계수를 이용하여 구한 식으로 나타나는 직선을 추정된 회귀직선이라고 합니다.
추정된 회귀직선
회귀계수에 대한 추정량 𝑏0, 𝑏1과 종속변수 Y의 예측값을 y^이라 하면, 추정된 회귀직선은 다음과 같습니다.

data("women")
women
plot(women$height, women$weight)
lines(women$height, women_lm$fitted.values)
women_lm <- lm(weight~height, data=women)
summary(women_lm)

회귀모형의 유의성 검정 (유의수준 0.05)
귀무가설: 종속변수와 독립변수 간 선형관계가 없다. (𝐻0: 𝛽1 = 0)
대립가설: 종속변수와 독립변수 간 선형관계가 있다. (𝐻1: 𝛽1 ≠ 0)
유의수준 0.05에서 p-value 값은 1.09e-14로 0에 가까운 수치를 보여준다. 따라서 귀무가설을 기각하고, 대립가설을 채택하게 된다. 즉, 종속변수와 독립변수 간 선형관계가 있다.
추정된 회귀직선(회귀계수)
Y = 3.45000X - 87.51667 + ε
결정계수(R^2)
• 결정계수는 0.9903로 독립변수가 종속변수의 변화량의 약 99%를 설명할 수 있음.
• 따라서 회귀 모형의 성능이 좋은 것으로 판단됨.
3. 잔차분석


Residual vs Fitted Plot
- 종속변수와 독립변수의 선형성을 파악할 수 있습니다.
- 본래 잔차와 적합값 사이에 무작위적인 형태 이외에는 어떠한 선형성도 보이면 안되나, 위 그래프에서는 이차 곡선이 보입니다.
그러므로 선형성 가정에 위반이 됨을 알 수 있고, 이처럼 어떠한 관계를 보일 때에는 회귀 모형에 2, 3차식 등의 다항식을 포함시키거나 로그나 루트를 씌어주는 등 변수 변환이 필요합니다.
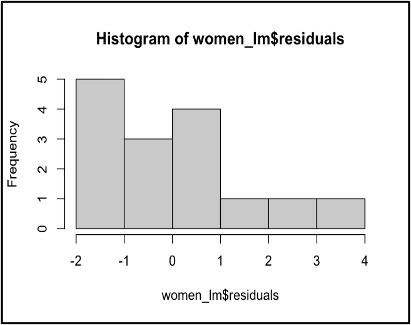
잔차의 정규확률 그림 (Normal Q-Q)
- 정규확률 그림은 x축으로는 이론적인 정규분포의 값, y축으로는 자료의 값을 갖는 산점도 입니다.
- 만일 자료가 정규분포를 따른다면 정규분포 적합선 위에 자료가 패턴 없이 많이 분포 합니다.
- 잔차의 정규성을 확인할 수 있습니다.
source
한빛 아카데미 - 제대로 알고 쓰는 R 통계분석
'Statistics' 카테고리의 다른 글
| [다변량분석] 회귀분석 - Prestige Data 잔차 분석, 모델 성능 비교 (0) | 2022.12.14 |
|---|---|
| [다변량 분석] 캐글 Mushrooms Data Classification (2) | 2021.09.29 |
| [다변량 분석] Survey Data를 이용한 다변량분석 (0) | 2021.09.29 |
| [다변량 분석] 검정 및 신뢰구간 추정 (1) | 2021.09.29 |
| statistics (2) | 2020.12.05 |


