| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- kt aivle school
- 소셜네트워크분석
- 가나다영
- KT 에이블스쿨
- SQLD
- 딥러닝
- ggplot2
- SQL
- 하둡
- 한국전자통신연구원 인턴
- 머신러닝
- cnn
- 다변량분석
- KT AIVLE
- 에이블러
- 지도학습
- 에이블스쿨
- arima
- dx
- Ai
- kaggle
- hadoop
- 빅데이터분석기사
- ML
- 시각화
- 프로그래머스
- 에트리 인턴
- r
- 빅분기
- 한국전자통신연구원
- 하계인턴
- ETRI
- matplot
- 시계열
- 서평
- Eda
- httr
- python
- 기계학습
- 웹크롤링
- Today
- Total
소품집
[ML] Decision Tree (의사결정 나무) 본문
Decision Tree

Decision tree는 머신러닝 중에서도 대표적인 지도 학습에 속합니다. 지도 학습이란, 모델 학습을 위해 '정답'이 주어진 데이터를 classification 하도록 만든 일종의 러닝 기술입니다. 즉 무언가를 결정할 수 있는 기준을 학습하는 것이 목표입니다.
Decision tree 가 'tree' 의 이름이 붙게 된 이유는, 나무를 뒤집어 봤을 때 닮아 붙여졌다고 하는데요. 그래서 제일 상단에 있는 하나의 노드는 루트 노드가 있고, 루트 노드를 시작으로 잔 가지를 branch 라 합니다. 하나 이상의 노드를 포함하고 있다면 하나 이상의 노드를 결정할 수 있어 Decision node라 하고, 반면 가장 말단에 있는 자식이 없는 노드를 leaf node(분류 종료) 라 합니다.

즉, 무언가를 '결정'할 수 있는 기준을 '학습'
결정 → 분류: '지금 보여주는 과일은 사과, 배 중에 무엇일까?

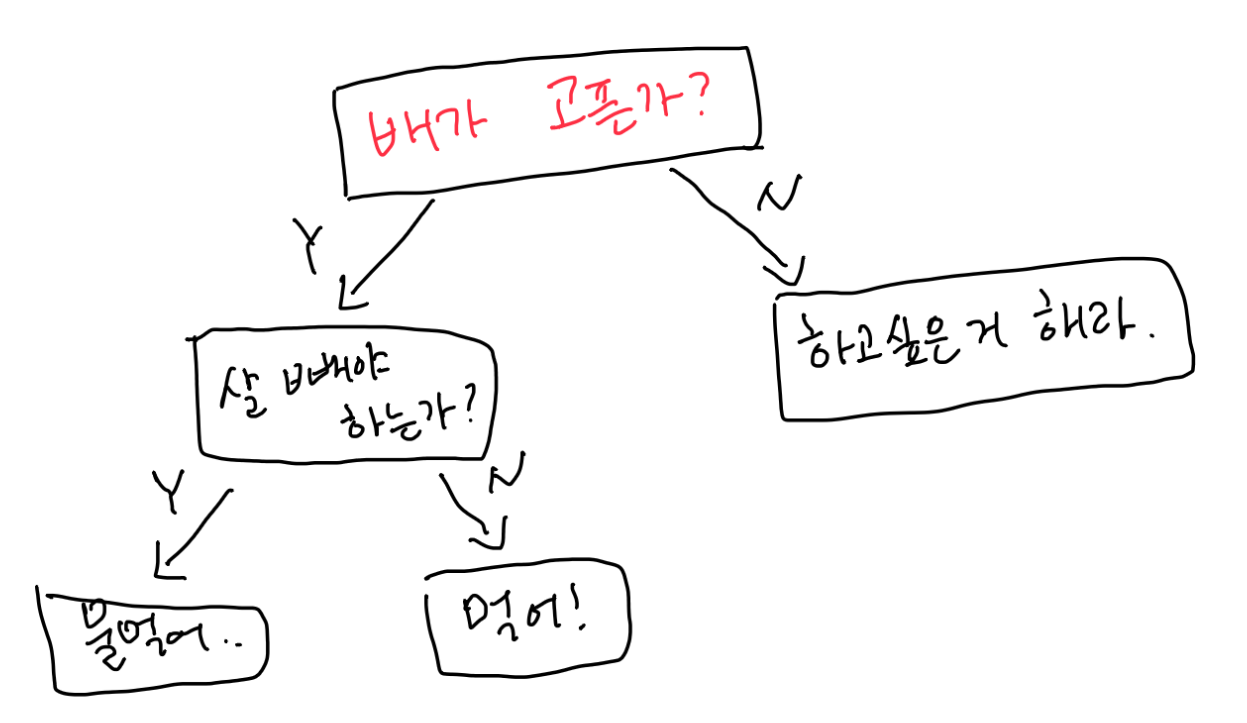
재미 삼아 그려본 제 의사결정 나무입니다.
이렇게 무언가를 '결정 → 분류'로 이어지는 선별 과정을 거쳐 학습하게 되는 것입니다.
상황, 데이터 예시
- 돈을 빌려줄지 말지를 결정할 때 어떤 기준을 세울 수 있을까?
- → ex) '돈 잘 갚아왔나?'. '갚을 상황은 되는가?' 등
- 기준들

새로운 사람이 돈을 빌리러 왔는데, 그 사람이 아래와 같을 때 돈을 빌려주는 '의사결정'을 해보자.
- +a, -c, +i, -e. +o, -u

좋은 트리의 구조
어떤 트리가 보다 더 좋은 트리라고 할 수 있을까요.
노드의 높이(길이)는 짧고, 말단 leaf node에서 하나의 값을 갖는 즉, 동일 라벨의 값을 갖고 있다면 좋은 tree로 분류 되었다고 할 수 있을 텐데요. 정리해서 말해보자면,
- Leaf node 에 통일된 label의 데이터로 분류됨 → 높은 정확도, 의사결정 정확도
- 빠른 수행 속도 → 트리의 높이가 짧은 것


깊은 노드로 분류가 정확하게 이루어진 왼쪽 트리와 classification은 약간 떨어지지만 노드가 짧은 오른쪽 트리.
두 개를 합칠 수 있다면 좋을텐데!
Decision Tree: 생성 알고리즘
트리 생성 방법
- 순서 : root node → leaf node
- root node는 모든 데이터를 고려한다고 가정
- 하위 노드(자식 노드)로 내려가면서 데이터가 분류됨
(1) 노드에서 고려할 데이터가 이미 하나의 class 에만 속해 있거나, 더 이상 고려할 feature 가 없다면 leaf node 로 여기고 자식노드를 생성하지 않고 멈춤. 만약, 고려할 feature 가 없어 leaf node가 된 경우, 가장 많은 수의 class를 결과 값으로 채택함.
(2) 각 노드에서 고려할 feature 선택시, 데이터들을 '가장 잘 나눠주는 feature' 를 선택하는 것이 중요
(3) 선택된 feature 에 대한 조건 별로(값마다) '자식 노드' 생성
(4) 각 '자식노드' 에서는 해당 조건을 만족하는 데이터만 고려하여 (1) 부터 반복수행
(2) 방법인 데이터들을 '가장 잘 나눠주는 feature' 를 선택하는 것이 중요한데요. 하지만 기계에게 최적된 값을 도출하는 feature를 골라달라는 것은 사실상 어려운 일이며, 완벽하게 나눠진다는 보장 또한 없습니다.
그래서 우리의 목적인 '가장 잘 나눠주는' feature를 정의하기 전에 'intuitive'하게 접근해보자
- 극단적인 case를 고려해볼까?
- 두 개의 class(A,B)가 있고, feature f가 {a,b} 중의 하나의 값을 가질 수 있는데, f=a 이면 class=A, f=b일 때 class=B인 데이터만 골라낼 수 있다면 어떨까?
- 즉, 고려중인 f=v에 대하여, 각 자식 노드에 '동일 class'에 속한 데이터들만 해당된다면 완벽하겠다!
Purity
- 한 쪽 데이터만 존재할 수록 more pure 하다!




그래서 feature를 정의하기 위해 가장 많이 사용되는 방법이 Entropy를 계산해 값을 비교해 보는 것입니다. Entropy 란, purity의 반대 개념으로 쓰이는데요, 즉 "엔트로피 값이 크다 == 더 난잡하다"라고 할 수 있죠.
트리 생성 시, 각 노드마다 어떤 feature를 고려할지 생각해볼 때, 당연히 자식 decision node가 가지는 데이터가 pure 할수록 좋다고 할 수 있습니다. 그래서 부모 노드의 purity와 자식 노드의 purity를 비교해서 그 차이가 더 클수록 좋은 feature로 선정될 수 있습니다.
Information Gain (정보함량) => 이 클수록, 변별력이 좋다!
- Information theory에서는 Entropy(impurity) == '정보의 함량' 이라고 보고 있음
- 부모노드 → 자식노드 방향으로 데이터가 흐르므로, 부모 노드에서 정보의 함량이 더 큼
- IG =부모노드의 Entropy - 자식노드의 Entropy
- 값의 범위는 0~1로 고정

결론적으로 '트리 생성 방법'을 정리해 보면,
(1) 노드에서 고려할 데이터가 이미 하나의 class 에만 속해 있거나, 더 이상 고려할 feature 가 없다면 leaf node로 여기고 자식 노드를 생성하지 않고 멈춤. 만약, 고려할 feature 가 없어 leaf node가 된 경우, 가장 많은 수의 class를 결과 값으로 채택함.
(2) 각 노드에서 고려할 feature 선택 시, 데이터들을 '가장 잘 나눠주는 feature'를 선택하는 것이 중요
→ information gain 이 가장 큰 feature 선택
(3) 선택된 feature에 대한 조건 별로(값마다) '자식 노드' 생성
(4) 각 '자식 노드'에서는 해당 조건을 만족하는 데이터만 고려하여 (1)부터 반복수행

Value 'bin'으로 트리 만들기!!

Tree 모양에 따른 용어
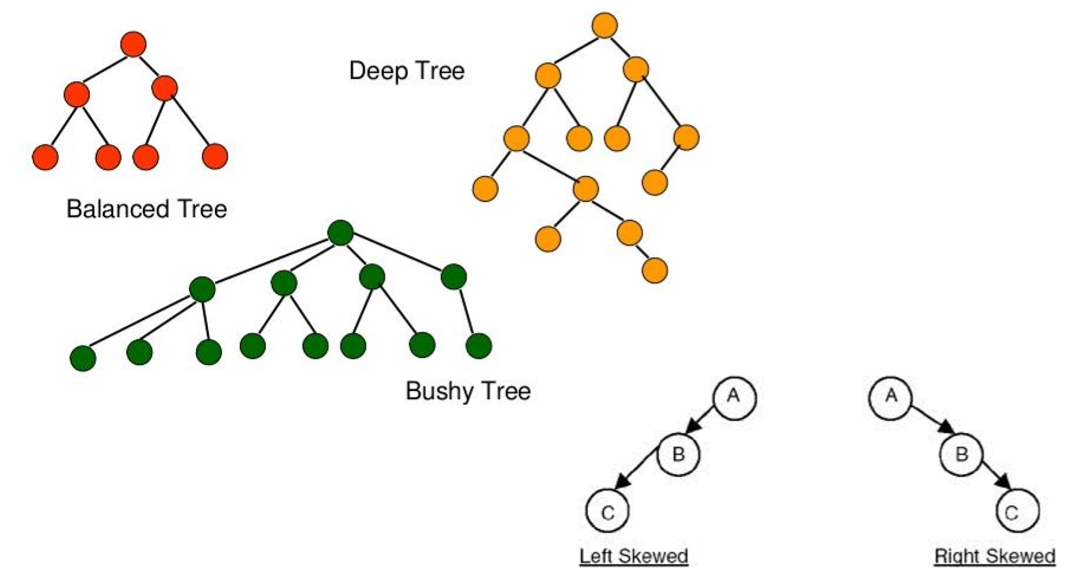
주의할 점!
지금은 큰 상관이 없지만, 그래프/트리 등으로 표현되는 알고리즘/모델들은 edge에 화살표 존재유무가 큰 의미를 가지므로 구분하여 사용하자!
질문

A. Decision tree는 오버피딩 되기 쉽다. 오버피팅은 틀렸는데, 맞았다고 예측하는 대표적인 오류다. 상단 노드에서 하단 노드로 내려갈 때 feature를 선택하게 되는데 두 개의 feature에서 선택값이 차이가 날 경우 오버피팅 나기 쉽상이다.

A. Decision tree를 생성할 때 정규화 과정은 필요하지 않다. 정규화를 거쳐도 같은 노드의 형태를 취하기 때문이다.
Decision tree의 장/단점
장점
- 시각적인 자료로 이해가 쉽다
- 변수의 정규화 및 표준화 과정이 필요하지 않음
- X, Y의 인과관계와 설명변수와 종속변수 간 영향력 파악 가능
단점
- 새로운 학습데이터를 적용할 시 낮은 어큐러시
- 단일결정 트리이므로 오버피팅이 발생할 확률이 높음 → 성능 저하
- 조금만 복잡한 문제를 해결하려 하면, 좋은 성능을 내기 어렵다.
ex) 비선형 문제의 XOR의 경우에도 Decision boundary를 잘 그려내지 못한다.
'AI' 카테고리의 다른 글
| [ML/DL] PCA, SVD, Linear Discriminant Analysis (0) | 2020.05.01 |
|---|---|
| [ML] Linear classification, regression (선형회귀) (0) | 2020.04.23 |
| [ML/DL] Data mining introduction (0) | 2020.04.22 |
| [ML] Gaussian Naive Bayes와 Bayesian Networks (0) | 2020.04.15 |
| [ML] 나이브 베이즈 정리 (0) | 2020.04.12 |




