| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- httr
- kaggle
- 기계학습
- kt aivle school
- 가나다영
- KT AIVLE
- Eda
- arima
- 하계인턴
- 한국전자통신연구원 인턴
- 한국전자통신연구원
- 다변량분석
- cnn
- 웹크롤링
- 빅분기
- 빅데이터분석기사
- 에이블스쿨
- SQL
- matplot
- 시계열
- 소셜네트워크분석
- 에트리 인턴
- 서평
- Ai
- 머신러닝
- dx
- r
- python
- 딥러닝
- ML
- 지도학습
- 시각화
- hadoop
- KT 에이블스쿨
- ETRI
- ggplot2
- 프로그래머스
- 하둡
- 에이블러
- SQLD
- Today
- Total
소품집
시계열 분해 알고리즘 - LOESS (MSTL) 본문
신재생 에너지 발전 중 태양광 발전 (Photovoltaic)은 셀 단위당 에너지 생산량이 증가하고 있고, 친환경적인 발전으로 많은 연구가 진행되고 있다. 정확한 단기 PV 발전량 예측은 전력 계통에서 원활한 에너지 수급과 공급을 조절할 수 있기 때문에 경제적인 측면에서도 중요하다.
이러한 PV 시스템은 일사량과 PV 발전소 특성 및 기상요인으로 인해 에너지 발전량의 차이가 나는데,
불확실성을 줄이기 위해 이전부터 고전 통계 모델 / 인공지능 모델 / 하이브리드 모델 등을 사용하여 예측 오차를 줄이려는 시도가 증가하고 있다.
다음 포스팅에서는 내가 연구하고 있는 데이터를 적용해보고,
먼저 이번 포스팅에서는 LOESS(MSTL)와 TFT를 공부해보려한다.
LOESS (MSTL)
* Multiple Seasonal-Trend Decompostion (다중 시계열 추세 분해)
MSTL은 단일 계절 성분을 추출할 수 있는 분해 방법인 STL (Seasonal-Trend Decomposotion using Loess)를 기반으로 한다. STL은 Loess(Locally Estimated Scatterplot Smooting)으로 평활법 기반이다.

Loess는 특정 y 값에서 주변 데이터의 window size에 다항식을 적합시켜 미래 예측값을 얻을 수 있고,
시계열 추세 모델링에 사용될 수 있음.

적절한 window size를 선택하면 Loess에서 시계열 추세를 확인할 수 있게 됨.
window size가 작을 경우 Loess가 계절성에 과적합되고, 반대일 경우에는 과소적합되는 경우가 생길 수 있음.
Example
import matplotlib.pyplot as plt
import datetime
import pandas as pd
import numpy as np
import seaborn as sns
from pandas.plotting import register_matplotlib_converters
from statsmodels.tsa.seasonal import MSTL, DecomposeResult
# 시각화 설정
register_matplotlib_converters()
sns.set_style('darkgrid')
plt.rc('figure', figsize=(16, 12))
plt.rc('font', size=13)t = np.arange(1, 1000)
daily_seasonality = 5 * np.sin(2 * np.pi * t / 24)
weekly_seasonality = 10 * np.sin(2 * np.pi * t / (24 * 7))
trend = 0.0001 * t**2
y = trend + daily_seasonality + weekly_seasonality + np.random.randn(len(t))
ts = pd.date_range(start="2020-01-01", freq="H", periods=len(t))
df = pd.DataFrame(data = y, index=ts, columns = ['y'])
df.head()df['y'].plot(figsize=(5, 3))
plt.show()
MSTL을 사용한 데이터 셋 분해
MSTL을 사용하여 시계열을 추세 / 일별 및 주별 계절 / 잔차 구성요소로 분해해보자.
mstl = MSTL(df['y'], periods = [24, 24*7]) # periods == 주기성 (각 1day, 7day)
res = mstl.fit()
res.seasonal.head()
ax = res.plot()
plt.show()
period 옵션으로 각 시간별 / 주별 계절성분이 추출된 것을 확인할 수 있다.
STL은 시계열 데이터에서 추세, 계절성 등을 분리하는 방법이고, MSTL은 이를 개선한 방법 중 하나이다.
MSTL에서는 주기(period)와 계절성(seasonal)을 제외한 다른 파라미터도 설정할 수 있는데,
직접 window size와 계절성 다항식 차수, 반복 횟수 등을 설정하며 세밀하게 조정해보자.
mstl = MSTL (
df,
periods = [24, 24*7],
windows = [101, 101],
iterate = 3,
stl_kwargs= {'trend' : 1001,
'seasonal_deg' : 0}) # 계절성을 이동 평균으로 적합시킥 위해 차수를 0으로 설정
res = mstl.fit()
ax = res.plot()
plt.show()
전력 수요 데이터 세트에 MSTL 적용
* 데이터 : 빅토리아 전기 수요 데이터 (2002년~2015년, 30분 단위로 기록된 총 전력 수요 데이터)
* 출처
https://arxiv.org/pdf/2107.13462.pdf
url = "https://raw.githubusercontent.com/tidyverts/tsibbledata/master/data-raw/vic_elec/VIC2015/demand.csv"
df = pd.read_csv(url)
df.head()
print(df.shape)timeseries = df[['ds', 'OperationalLessIndustrial']]
timeseries.columns = ['ds', 'target'] # rename
# 2012년 149일만 가져와보장.
start = pd.to_datetime('2012-01-01')
end = start + pd.Timedelta('149D')
mask = (timeseries['ds'] >= start) & (timeseries['ds'] < end)
timeseries = timeseries[mask]
timeseries = timeseries.set_index('ds').resample('H').sum()
timeseries.head()
MSTL을 반영한 전력 수요 분해
mstl = MSTL(timeseries['target'], periods = [24,24*7], iterate = 3,
stl_kwargs={'seasonal_deg' : 0,
'inner_iter' : 2,
'outer_iter' : 0})
res = mstl.fit()
ax = res.plot()
plt.tight_layout()
plt.show()
res.seasonal.head() # 계절 성분 확인 !
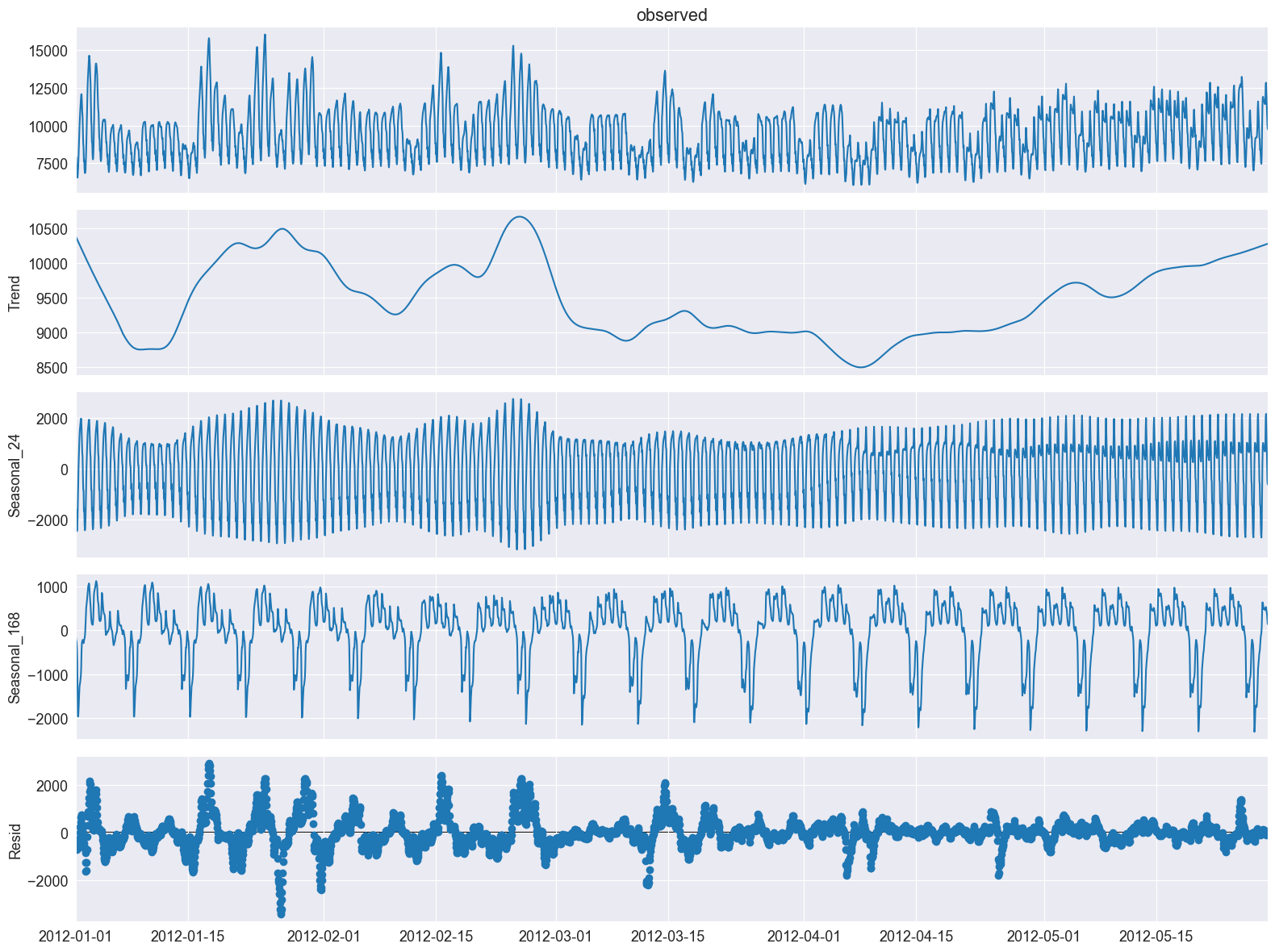
계절 성분 요소를 더 자세히 살펴보고, 일일 및 주간 계절성을 확인해보자.
fig, ax = plt.subplots(nrows=2, figsize=[10, 10])
res.seasonal['seasonal_24'].iloc[:24*3].plot(ax = ax[0])
ax[0].set_ylabel('seasonal_24')
ax[0].set_title('Daily seasonality')
res.seasonal['seasonal_168'].iloc[:24*7*3].plot(ax = ax[1])
ax[1].set_ylabel('seasonal_168')
ax[1].set_title('Weekly seasonality')
plt.tight_layout()
plt.show()
일별 전력수요의 계절성을 잘 반영하고 있는 것을 확인할 수 있고,
주간으로 보면 주말에는 전력 사용량이 적은 것을 확인할 수 있음.
다음으로는 MSTL 장점 중 하나인, 시간이 지남에 따라 변하는 계절성을 확인할 수 있 것을 확인해보자.
fig, ax = plt.subplots(nrows=2, figsize=[10, 10])
mask = res.seasonal.index.month==5
res.seasonal[mask]['seasonal_24'].iloc[:24*3].plot(ax=ax[0])
ax[0].set_ylabel('seasonal_24')
ax[0].set_title('Daily seasonality')
mask = res.seasonal.index.month==5
res.seasonal[mask]['seasonal_168'].iloc[:24*7*3].plot(ax=ax[1])
ax[1].set_ylabel('seasonal_168')
ax[1].set_title('Weekly seasonality')
plt.show()

자정 시간대에 다른 패턴도 나오는 것을 확인할 수 있음!
ref.
https://www.statsmodels.org/dev/examples/notebooks/generated/mstl_decomposition.html
'Time series' 카테고리의 다른 글
| Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting 리뷰 (0) | 2024.03.18 |
|---|---|
| ARIMA models (0) | 2020.06.22 |
| ARMA model - 자기회귀이동평균 (0) | 2020.06.22 |
| ARMA model (0) | 2020.06.20 |
| 이동평균모형 (Moving average models : MA) 식별법 (0) | 2020.06.12 |



