| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- 다변량분석
- r
- Eda
- 빅데이터분석기사
- KT 에이블스쿨
- Ai
- SQL
- 에이블스쿨
- ML
- 소셜네트워크분석
- 한국전자통신연구원
- dx
- 하둡
- 에트리 인턴
- kt aivle school
- 서평
- 에이블러
- 웹크롤링
- 머신러닝
- 시계열
- matplot
- 기계학습
- arima
- 가나다영
- 빅분기
- 지도학습
- 하계인턴
- kaggle
- 시각화
- 프로그래머스
- ggplot2
- ETRI
- SQLD
- 한국전자통신연구원 인턴
- hadoop
- KT AIVLE
- python
- 딥러닝
- cnn
- httr
- Today
- Total
소품집
ARIMA models 본문
#ARIMA models
ARIMA(Autoregressive Integrated Moving Average Models)
ARIMA (p,d,q) models

- Φ(B) 는 차수가 p인 B의 다항식: Φ(B) = 1+ Φ1B + Φ2 B2 + … + Φp Bp
- 𝜃 (B) 는 차수가 q인 B의 다항식: 𝜃 (B) = 1+ 𝜃1B + 𝜃2B2 + … + 𝜃𝑞B
- AR: p → 자기회귀모형의 차수
- I: d → 차분한 횟수
- MA: q → 이동평균모형의 차수
Sepecoal cases
- ARIMA(0,0,0): 백색잡음 (white noise)
- ARIMA(0,1,0) with no constant : 랜덤워크 (Random walk)
- ARIMA(0,1,0) with constant: 절편항 (drift term)이 있는 랜덤워크
- ARIMA(p,0,0): 자기회귀모형 AR(p)
- ARIMA(0,0,q): 이동평균모형 MA(q)
ARIMA(p,d,q) models
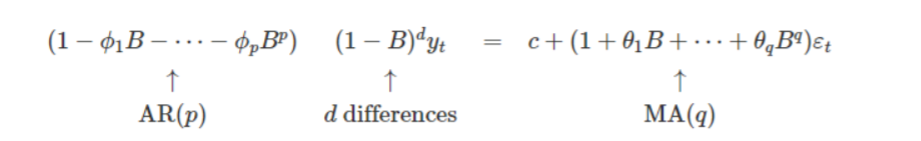
yt-M = zt라 두면 다시 위와 같이 정리되는 것을 알 수 있다.



위 식에서 만약 차분을 하지 않게되면 intercept form과 mean form에 차분 횟수(d)를 0으로 넣어주면 됩니다.
ARIMA 모형 시뮬레이션
arima.sim() 함수를 통해 AR, MA, ARMA, ARIMA 확률과정을 따르는 데이터를 생성할 수 있다. 정답을 알고 있는 상황에서 ARIMA모형을 식별할 수 있다.
set.seed(1234)
arima_1_1_1 <- arima.sim(model=list(order=c(1,1,1),**ar=0.7,ma=-0.2**),n=300)
ggtsdisplay(arima_1_1_1)
summary(ur.kpss(diff(arima_1_1_1)))
# 정상시계열이 아니다.-> 차분하여 정상시계열을 만족하게 해야한다.
# ACF와 PACF를 보고 AR과 MA의 차수를 결정해야 한다.

- 유의수준 1%에서 임계값 0.739
- 검정통계량 4.009
- 검정통계량이 임계값을 벗어나므로 귀무가설(=정상시계열이다)기각
- 따라서 정상시계열이 아니다.
위의 kpss검정을 통해 정상시계열이 아닌 것을 확인할 수 있습니다.
또한 좌측의 ACF 그래프를 보면, 모든 값이 신뢰구간을 넘어서는 값을 보이고 있습니다.
그래서 ACF(자기회귀)와 PACF(부분자기회귀) 그래프를 보며 AR과 MA, 그리고 차분 횟수까지 결정해주며 변동값을 확인하며 적절한 횟수를 결정해야합니다.
arima_fit <- Arima(arima_1_1_1, order=c(1,1,1)) # 시뮬레이션 모델을 Arima에 적합
ggtsdisplay(diff(arima_1_1_1)) # 차분 - 잔차가 정상시계열을 만족하는 것을 확인할 수있다.
checkresiduals(arima_fit)

위의 그래프로 checkresiduals를 통해 잔차를 확인해보면, 유의확률(p-value)이 유의수준 0.05보다 큼으로 귀무가설(자기상관성은 없음)을 채택하게 된다.
# ARIMA 모형 시뮬레이션
arima_F <- forecast(arima_fit)
autoplot(arima_F) + autolayer(arima_F$fitted)
summary(arima_F)

#ARIMA modeling in R
auto.arima()는 어떻게 작동되는가?

auto.arima()는 정보손실을 기준으로 적합될 값을 추천해주는데, AICc가 작을수록 적합이 더 잘 된것임을 알 수 있음. 즉 정보를 손실량을 줄인 적합방법으로 쓰일 수 있다.
하지만 항상 최선의 값을 반환해주는 것이 아니기 때문에 이를 명심하자~!
일반적인 ARIMA 모형 구축 절차

Arima()에서 상수항(constants)처리 방법
- d=0일 때
- yt의 평균값으로 추정
- d>0일 때
- c = μ= 0 으로 추정
- include.mean (기본값은 TRUE)
- d=0일 떄만 추정됨
- include.mean=FALSE → c=μ= 0
- include.drift (기본값은 FALSE)
- d=1인 경우, μ≠0으로 허용 (drift라고 불림)
- d >1 인 경우, 허용 안 함
- include.constant
- 만일 TRUE이고, d=0이면 include.mean =TRUE, d=1이면 include.drift=TRUE로 정해짐
- 만일 FALSE이고, include.mean과 include.drift는 FALSE로 정해짐
Arima()에서 상수항 (constants)이해하기

Source
https://statkclee.github.io/finance/stat-time-series-arma.html#4_추억의_arima
'Time series' 카테고리의 다른 글
| Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting 리뷰 (0) | 2024.03.18 |
|---|---|
| 시계열 분해 알고리즘 - LOESS (MSTL) (0) | 2023.12.15 |
| ARMA model - 자기회귀이동평균 (0) | 2020.06.22 |
| ARMA model (0) | 2020.06.20 |
| 이동평균모형 (Moving average models : MA) 식별법 (0) | 2020.06.12 |



